Solución de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (20 de enero de 2003)
Problema nº 17.- Propiedades del triángulo órtico.
“Tenemos que demostrar en primer lugar un postulado que concierne al triángulo órtico. afirmamos que los ángulos AFG y CFE son iguales, y que consecuentemente los ángulos semejantes en E son iguales y asimismo lo son aquellos en G...” (Hermann Amandus Schwarz).
Solución.-
Que los ángulos AFG y CFE
sean iguales, equivale a decir que sus complementarios también lo sean, esto
es, que la altura BF sea la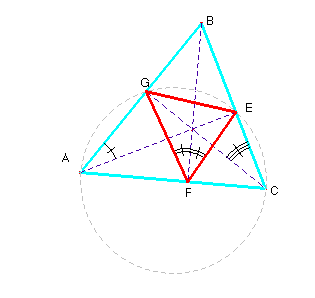 
bisectriz del ángulo F del triánguo órtico.
En resumen, lo que hemos de probar es que las alturas de un triángulo acutángulo
son las bisectrices de su triángulo órtico.
En efecto, los triángulos rectángulos AGC y AEC tienen la misma hipotenusa, el lado AC, luego los puntos A, G, E y C son concíclicos, y por ello, los ángulos 1= GAE y 3= GCE son iguales por abarcar el mismo arco.ç
Razonando de forma similar, por ser concíclicos los puntos GFCB, concluimos que son iguales los ángulos 2= GFB y 3= GCE. Por último también resultan iguales los ángulos 1= GAE y 4=BFE. (En el dibujo son iguales los ángulos marcados).
Y con esto demostramos que BF es la bisectriz del ángulo F en el triángulo órtico y concluimos.