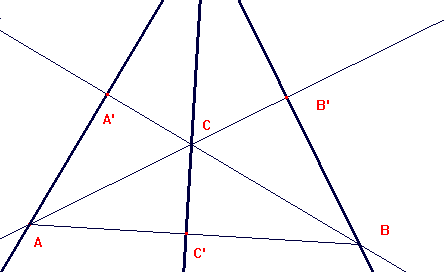
Problema 4. Caso obtusángulo
| altura. La altura de un triángulo (correspondiente a un lado) es la recta perpendicular que pasa por el vértice opuesto. Las tres alturas de un triángulo se cortan en el ortocentro |
Tenemos el triángulo ABC obtusángulo en C.

Tracemos las tres alturas, AB', CC`y BA'.
Apliquemos el teorema de Ceva (ver problema 37), que es:
| Teorema de Ceva. Sean a, b c, los vértices de un triángulo y tres puntos a' de bc, b' de ca, y c' de ab sobre los lados de este triángulo. Entonces las tres rectas aa', bb', y cc' son concurrentes si y sólo si se tiene: a'b / a'c b'c / b'a c'a/ c'b = - 1 |
Tenemos que los triángulos CC'A y BB'A, por una parte,
y los CC'B y AA'B por otra , son semejantes, por tener ángulos iguales.
Luego, es: CC'/B'B = AC'/AB', y CC'/A'A = BC'/BA'
es, dividiendo la primera igualdad por la segunda,
A'A/B'B = AC'/AB' BA'/BC' [1].
También los triángulos A'AC y B'BC son semejantes,
por ser rectángulos en A' y B' y común el ángulo en C.
Luego, es: B'B/A'A = CB'/ CA', por lo que es, teneindo en cuenta [1], que:
CA'/CB' = AC'/AB' BA'/BC', por lo que:
(A'B B'C C'A )/(A'C B'A C'B) = 1, y si tenemos en cuenta la orientación, es -1., luego,
c.q.d. las tres alturas de un triángulo obtusángulo se cortan en un punto,
llamado ortocentro.