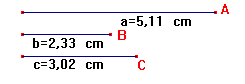
Sean a, b, c la longitud de las alturas. En el applet siguiente pueden modificarse desde los puntos A, B, C.
Aunque el procedimiento de construcción del triángulo pueda parecer algo artificial, funciona, y es de fácil justificación.
Figura: alturastriangulo1.fig
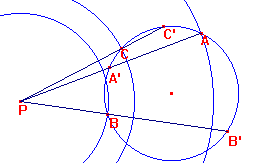
Se toma un punto cualquiera P y una circunferencia auxiliar. Sobre ella se hace la construcción típica de potencia de un punto respecto a la circunferencia, siendo PA = a;....obteniendo los puntos A, B, C. y los puntos A', B', C'.
|
|
|
Las circunferencias de radios, a,b,c con centro en P, han de cortar a la circunferencia auxiliar. Si no cortan será preciso mover P o bien el tamaño de la circunferencia auxiliar.
Construimos un triángulo con los segmentos PA'=a', PB'=b', PC'=c' (construcción elemental). Se verifica, que este triángulo es semejante al triangulo pedido.
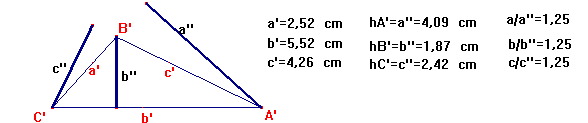
Sean a'', b'', c'', las alturas del triangulo de lados, a', b', c'.
Por un lado tenemos, por potencia de un punto sobre una circunferencia:
a . a' = b . b' = c . c' =Constante
y sobre el triangulo de lados a', b', c' y alturas a'', b'', c'':
a' . a'' = b' . b'' = c' . c'' = 2(área del triángulo)
dividiendo miembro a miembro tenemos;
a/a'' = b/b'' = c/c''= cte.
como puede verse en el applet CabriJava.
Esto es, las alturas a'',b'',c''de este triángulo son proporcionales a las alturas dadas a,b,c . Si hacemos un triángulo semejante de razón la cte calculada, el problema está resuelto.
Esta construcción esta tomada de:
-Rendón Gómez, A. Geometría paso a paso. Pág. 172.. Ed. Tébar
- Sánchez Vázquez, G. Métodos Gráficos de resolución de problemas geométricos. Pág. 93. Sociedad Andaluza de Educación Matemática "THALES"
Solución dada por Jose M Arranz
Centro de Profesores y Recursos de Ponferrada (León).