192.
Teorema: En todo triángulo, la bisectriz de un ángulo “interior” divide al
lado opuesto en dos segmentos aditivos directamente proporcionales a los lados de dicho
ángulo. |
Bruño
(1.950): Tratado de Geometría. Bruño.
Madrid. (pag 104)
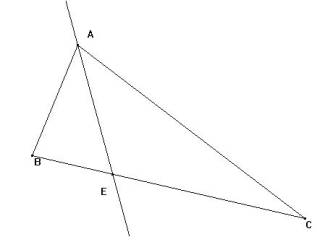
Demostración:
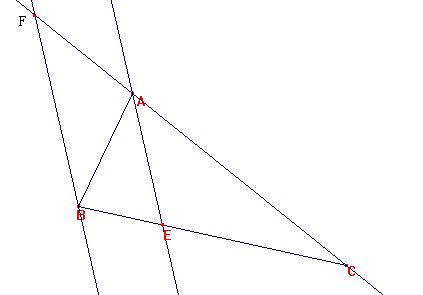
Si trazamos una paralela a AE por B, nos cortará a la recta AC en F. Tenemos las siguientes propiedades:
- el ángulo AFB es igual al CAE por ser ambos constituidos por la recta AC cortada por paralelas
- el ángulo ABF es igual al BAE por ser alternos internos entre paralelas
- el triángulo BAF es isósceles y por tanto, AF=AB.
- los triángulos CEA y CBF son semejantes al tener los tres ángulos iguales.
- Luego es:
