355. Demostrar que en todo triángulo la bisectriz se encuentra entre la mediana y la altura trazadas desde el mismo vértice

Lidski, V. y otros (1.978): Problemas de Matemáticas Elementales. Editorial Mir. Moscú (pag 57)

Soluciones de Samuel Pérez Martínez

Demostración: Sean BD, BE y BF, respectivamente, una altura, una bisectriz y una mediana en el triángulo ABC. Al ángulo de vértice A y lados AB AC, lo denotaremos por BAC

Supongamos que AB < BC. Debido a que en un triángulo, a lado mayor se opone ángulo mayor (1),

tenemos: BAC > BCA , CBD > ABD, de donde:

CBD > 1 /2 ( ABD + CBD) = 1 /2 B.

Por lo tanto la bisectriz BE pasa por dentro del ángulo CBD

y el punto E se encuentra entre D y C.

Por otra parte, es(ver problema 1), AE /EC = AB / BC < 1, de donde, AE < EC.

De lo anterior, AE < 1 /2 (AE + EC ) = 1/ 2 AC. O sea, AE < AF.

Por consiguiente, el punto F se encuentra entre E y C.

Así pues, el punto E se encuentra entre D y F, c.qd.

(1) En todo triángulo, a lado mayor se opone mayor ángulo.

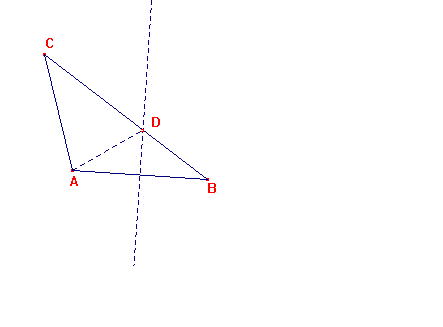
Supongamos BC>AC. La mediatriz de AB cortará a CB en un punto interior D, debido a que por construcción se forma ADB isósceles, y en el triángulo ACD, es AC < AD+DC = BD+DC.

Tenemos por construcción que DAB = DBA, y por ello,

CAB = CAD + DAB >.DAB = DBA, c.q.d.