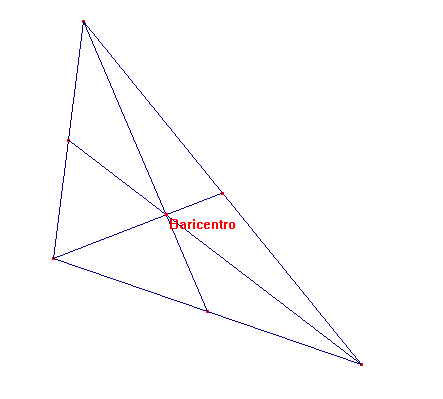
6.4.3. Teorema 2 “Las medianas de un triángulo se cortan en un punto que se encuentra a los dos tercios de la distancia comprendida entre un vértice y el punto medio de lado opuesto”

Sánchez,M.(1.983): Geometría sin esfuerzo. Círculo de Lectores. Bilbao (pag 147)

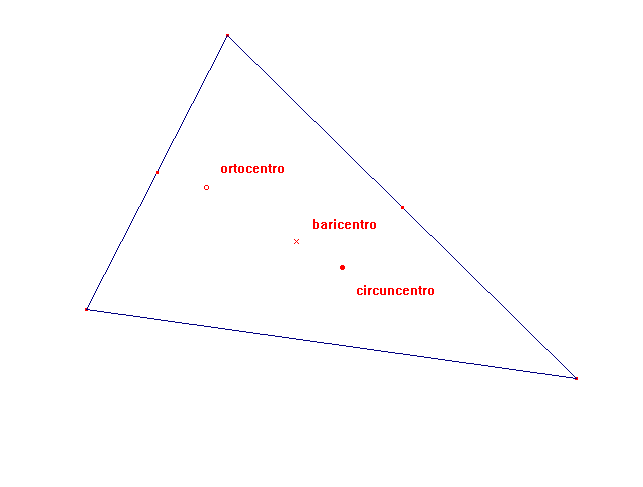
Teorema de la recta de Euler. En cualquier triángulo, el circuncentro, el baricentro y el ortocentro son colineales y la distancia del baricentro al ortocentro es doble de la distancia del baricentro al circuncentro

Eccles, F.M. (1.999): The Euler Line and Nine-point-circle Theorems. The Mathematics Teacher (January). Vol 92, nº 1. (pp 50-54)

Teorema del círculo de los nueve puntos. En cualquier triángulo, los puntos medios de los lados, los pies de las alturas, y los puntos medios de los segmentos que unen los vétrices al ortocentro, están en el círculo cuyo radio es la mitad del radio del círculo circunscrito y cuyo centro está en el punto medio del segmento que une el ortocentro al circuncentro.

Eccles, F.M. (1.999): The Euler Line and Nine-point-circle Theorems. The Mathematics Teacher (January). Vol 92, nº 1. (pp 50-54)