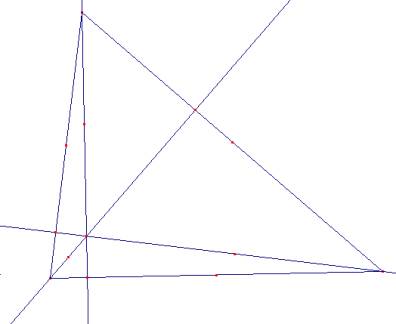
mediana. Una mediana de un triángulo es una recta que pasa por un vértice y por el punto medio del lado opuesto. Las tres medianas se cortan en el centroide o baricentro.

altura. La altura de un triángulo (correspondiente a un lado) es la recta perpendicular que pasa por el vértice opuesto. Las tres alturas de un triángulo se cortan en el ortocentro.

circuncentro. El circuncentro de un triángulo es el centro de la circunferencia circunscrita al triángulo. Es el punto O de la figura en el que se cortan las perpendiculares a los lados en su punto medio o mediatrices.

incentro. El incentro de un triángulo es el centro de la circunferencia inscrita. Es el punto en el que coinciden las tres bisectrices interiores de los ángulos del triángulo.

Clapham, C. (1.992): Diccionario Oxford de Matemáticas. Celeste Ediciones. Madrid. (pags 5, 150, 30 y 125). (Traducción de Alfonso Carlos Casal Piga y José Manuel Vegas Montaner)

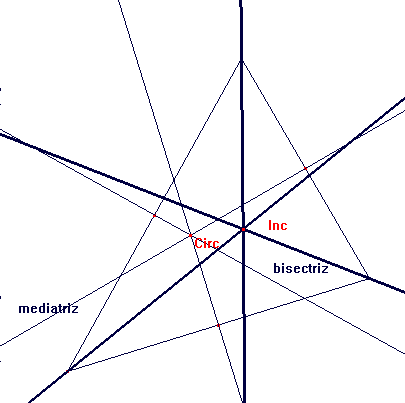
124 Recta de Euler: Demostrar que en un triángulo arbitrario, el punto de intersección de las alturas, el punto de intersección de las medianas y el centro de la circunferencia circunscrita, están situados en una recta. Esta recta se llama recta de Euler.

125. Circunferencia de Euler: Demostrar que en un triángulo arbitrario, las bases de las medianas, las bases de las alturas, y también los puntos medios de los segmentos que unen el punto de intersección de las alturas del triángulo con sus vértices, están situados en una circunferencia. Esta maravillosa circunferencia se llama a veces circunferencia de Euler

Nesterensko, Yu. V., Olejnik, S.N. y Potápov, M.K. (1.994): Antiguos Problemas Recreativos en Rusia. Servicio Editorial Universidad Del País Vasco. (pag 85) (Traducción de Elena Aparicio Cortés, revisada por Emiliano Aparico Bernardo).

Leonard Euler (1.707-1.783). Ohio State University Libraries. En Dunham, W. (1.990): Journey througt Genius (The Great Theorems of Matematics). Wiley. Nueva York (pag 209)