Problema 11. Solución de la alumna Maite Peña Alcaraz del Colegio Portaceli de Sevilla (17 de febrero de 2003)
| Teorema de la recta de Euler. En cualquier triángulo, el circuncentro, el baricentro y el ortocentro son colineales y la distancia del baricentro al ortocentro es doble de la distancia del baricentro al circuncentro |
Eccles, F.M. (1.999): The Euler Line and Nine-point-circle Theorems. The Mathematics Teacher (January). Vol 92, nº 1. (pp 50-54)
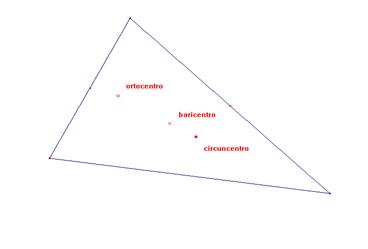
La demostración de que estás alineados, cojo la misma que di al problema último que te mandé.
La copio a continuación:
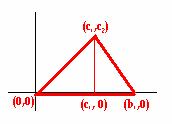
Si colocamos de esa manera en los ejes cartesianos un triángulo cualquiera y averiguamos su baricentro, su circuncentro y su ortocentro.

Y para ver si están alineados simplemente hay que ver si se cumple:
![]()
Entonces si lo aplicamos obtenemos:
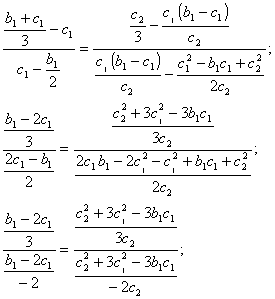
Lo que es evidente que se cumple, luego está demostrado que el baricentro G, el circuncentro C y el ortocentro O, de un triángulo cualquiera están alineados.
Ahora me dispondré a dar la otra demostración:
Si sacamos el vector director GO y el vector director GC para averiguar el módulo y comprobar si una de las distancias es doble que la otra obtenemos: (Como aclaración el vector director se consigue restándole a las “x” de un punto las del otro y a las “y” del mismo punto las del otro.
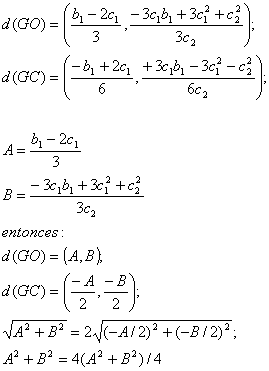
Y como eso es evidente, queda demostrado.