PROBLEMA 12

Solución de Nicolás Rosillo Fernández.

Dpto. Matemáticas, IES Máximo Laguna.

Santa Cruz de Mudela, Ciudad Real

nrosillo@olmo.pntic.mec.es

12.- El centro de la circunferencia de Euler está en la recta de Euler situado en el punto medio entre el ortocentro y el circuncentro.

Dado que circuncentro y ortocentro pertenecen a la recta de Euler, el problema se reduce a demostrar que el centro de la circunferencia de Euler es el punto medio entre ortocentro y circuncentro.

En su magnífico libro “La experiencia de descubrir en geometría” (Ed. Nivola), Miguel de Guzmán da los siguiente resultados para el programa de cómputo simbólico DERIVE:

Coordenadas del ortocentro en función de los vértices (m,n) (p,q) y (r,s) del triángulo

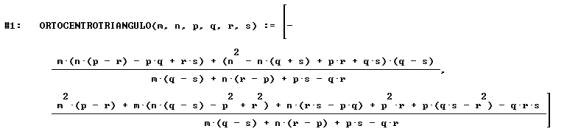
Coordenadas del circuncentro en función de los vértices (m,n) (p,q) y (r,s) del triángulo

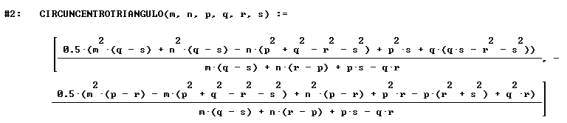
Coordenadas del centro del círculo de Feuerbach en función de los vértices (a,b) (c,d) y (e,f) del triángulo

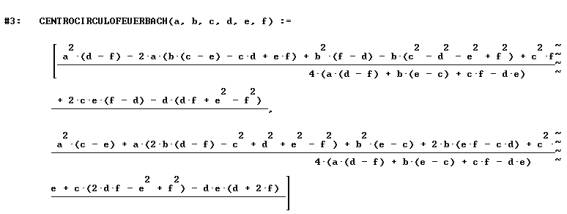
Si se pide al programa DERIVE que calcule las coordenadas del punto medio de ortocentro y circuncentro

DERIVE devuelve la siguiente expresión:

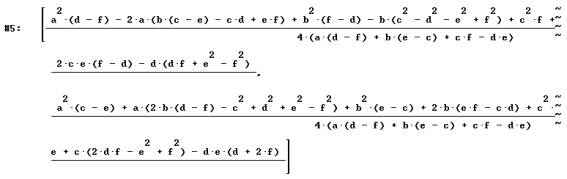
expresión que restada a la de las coordenadas del centro del circulo de Feuerbach

da como resultado (0,0), lo que implica la igualdad y demuestra el problema.