Problema nº 14.- Segundo punto de Fermat, F’. La construcción es muy parecida a la de F. La única diferencia es que los tres triángulos equiláteros se dirigen hacia dentro, como en la figura. (Truscott, B. (1.997): A new geometry result: the Lester circle. Pythagoras,nº 43 Agosto pp 26)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca(7 de Enero de 2004).-

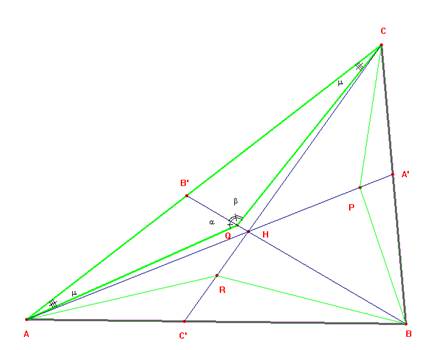
Realizando giros de centros A, B y C y amplitud de 60º transformamos los triángulos ABB’, BC’C y CA’A en los triángulos AC’C, BAA’ y CBB’ respectivamente, resultando, por tanto iguales los segmentos AA’, BB’ y CC’ y que las rectas AA’, BB’ y CC’ forman entre sí ángulos de 60º y 120º.

Para ver finalmente que las rectas son concurrentes si llamo F = BB’∩CC’ y F’ = AA’∩CC’ como el ángulo CFB’ =120º, resulta que el cuadrilátero FCAB’ está en la circunferencia que circunscribe al triángulo AB’C.

De igual modo, como áng.(CF’A)=60º, F’, B’, A y C son concíclicos, pues están sobre el arco capaz de AC y ángulo 60º, esto es, sobre la circunferencia circunscrita al triángulo AB’C. Tenemos, pues, sobre la misma circunferencia los puntos A, B’, C, F y F’; F y F’ están alineados con B’; esto sólo es posible si F = F’.

2º demostración: Haremos uso del teorema de Ceva. Vamos a calcular el valor de Ceva. Demostraremos, de forma más general que al construir sobre cada lado, hacia el interior, triángulos isósceles semejantes, las rectas que unen cada vértice con el opuesto del triángulo adherido a él son concurrentes en un punto.

Vamos a calcular el valor del cociente . Las áreas de los triángulos con igual altura son proporcionales a las bases, por tanto, el cociente anterior es igual a la razón de las áreas de los triángulos B’QC y B’QA.

Si tomamos como bases los lados QC y QA respectivamente, tendremos: Área(B’QA) = ½· QB’· QA· sena; y Área(B’QC) = ½· QB’· QC ·sen b; pero como QA = QC, se tiene, en resumen:

En los triángulos QBA y QBC con QB como lado común, aplicando el teorema de los senos tenemos: y ; despejando sen a y sen b y sustituyendo estas expresiones en la razón entre las áreas resulta, finalmente: . Permutando convenientemente las letras A, B y C, se obtienen:

y . El producto de estas tres razones es: , que demuestra la concurrencia.

En particular: Si m = 60º, el punto de concurrencia H es el segundo punto de Fermat. c.q.d. (Si el ángulo m coincide con alguno de los ángulos del triángulo ABC el problema carece de sentido y la construcción anterior no sirve.)