15. Para comenzar, tomemos un triángulo no isósceles, ABC. Relacionado con él, construyamos cuatro puntos especiales, que de acuerdo con el teorema de Lester, todos están sobre un círculo. Los estudiantes conocen que tres puntos no colineales determinan un círculo, así que cuando cuatro puntos especiales están sobre un círculo, ¡entonces tenemos un teorema!

Los cuatro puntos son los siguientes: Circuncentro, punto de Fermat, segundo punto de Fermat, centro del círculo de Euler.

Solución del profesor Nicolás Rosillo Fernández, IES Máximo Laguna (Santa Cruz de Mudela, Ciudad Real).

Sea nuestro triángulo de vértices (0,0), (a,0) y (b,c). Utilizamos DERIVE.

Realicemos los cálculos necesarios para preparar la obtención de los puntos de Fermat:

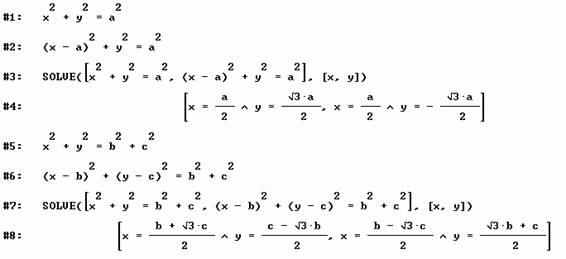
Obtengamos ahora las coordenadas del primer punto de Fermat

Y del segundo punto de Fermat

Basándonos en las expresiones que Miguel de Guzmán da en su libro "La experiencia de descubrir en geometría" para el circuncentro

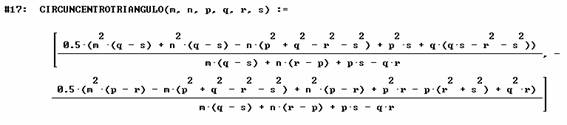
el centro del circulo de Feuerbach (o de Euler)

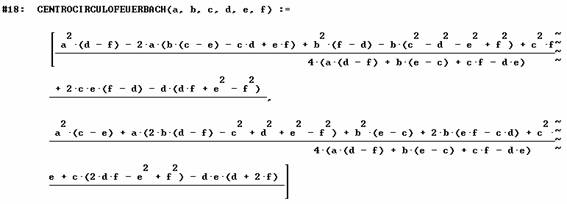
y la expresión de una circunferencia que pasa por tres puntos

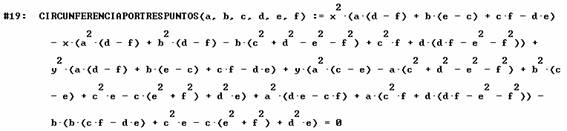
Se calculan entonces circuncentro y el centro del circulo de Feuerbach para nuestro triángulo original, y se introducen sus coordenadas junto a las del primer punto de Fermat para hallar la ecuación de la circunferencia que pasa por esos tres puntos

Al sustituir x e y por las coordenadas del segundo punto de Fermat, y simplificar, se obtiene la expresión 0=0.

Nicolás Rosillo Fernández

4 julio 2006