Problema nº 18.- Las circunferencias de Apolonio. Los puntos isodinámicos.

Dado un triángulo ABC, tracemos por A sus bisectrices interior y exterior. Cortarán a la recta BC en dos puntos, B’ y C’. La circunferencia de diámetro B’ C’ se denomina de Apolonio. Las tres circunferencias de Apolonio de un triángulo se cortan en los puntos isodinámicos.  

Solución del profesor Saturnino Campo Ruiz, del IES Fray Luis de León de Salamanca (23 de Junio de 2003).-

Para probar que las tres circunferencias de Apolonio de un triángulo se cortan en dos puntos (los puntos isodinámicos) necesitamos, previamente, algunos resultados:

a)                 Teorema de la bisectriz.- En todo triángulo, la bisectriz de un ángulo y la del ángulo externo correspondiente dividen al lado opuesto en dos segmentos proporcionales a los lados del ángulo.

Recíprocamente: Si una recta trazada desde un vértice de un triángulo divide el lado opuesto en partes proporcionales a los lados adyacentes, es bisectriz del ángulo del triángulo o del ángulo externo, según que divida interior o exteriormente al lado opuesto.

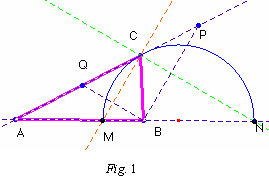
En efecto: llevemos sobre la recta AC y a ambos lados de C los segmentos CP = a = CQ. Al ser isósceles el triángulo BCP, la bisectriz CN es perpendicular a la base BP. Como también lo es a la otra bisectriz CM, resulta que los segmentos CM y PB son paralelos. Aplicando el Teorema de Thales :                                                                              

.

Con el mismo razonamiento sobre el triángulo isósceles QCB, concluimos que también son paralelos los segmentos QB y CN. Y aplicando otra vez el teorema de Thales se obtiene   c.q.d.

Recíprocamente, si la recta CM dividiera al lado AB en partes proporcionales a los otros lados y no fuera bisectriz, se podría trazar una recta desde C que si lo fuera, y por el teorema directo habría de dividir al lado AB en partes proporcionales a b y a a. Pero en AB no puede haber más que un punto que lo divida en esa relación, (Los puntos X de AB cuya razón de distancias a A y B es k se obtienen tomando x = d(A,X)=d(A,B)· ) y,  siendo ese punto por hipótesis el punto M, la recta CM tiene que confundirse con la bisectriz.

Para el caso de que la recta divida exteriormente al lado, el razonamiento es similar.

Del teorema de la bisectriz se deduce que los puntos alineados A, B, M y N  forman una cuaterna armónica, pues  y a la inversa, si la (A B M N) = -1 y CM no es bisectriz de  ACB existe B’ sobre MN de modo que CM es la bisectriz de ACB’ y según hemos visto sería (A B’ M N) = -1; pero como también es  (A B M N) = -1 y el cuarto armónico es único, B = B’.

b)El lugar geométrico de los puntos cuya razón de distancias a dos puntos dados es una constante distinta de la unidad es una circunferencia (la circunferencia de Apolonio de esos puntos).

Dados A y B (fig. 1), sobre la recta que determinan hay dos puntos M y N  para los cuales  Si C es un punto genérico del lugar, es decir, C varía de modo que , al ser constante esa razón, serán constantes también los pies de las bisectrices interior y exterior de ACB, los puntos M y N, pues son los únicos puntos de la recta AB cuya razón de distancias a A y B es precisamente k, y como estas bisectrices son mutuamente perpendiculares, los puntos C del lugar están en la circunferencia de diámetro MN.

Recíprocamente, si C está en esa circunferencia, como CM y CN son perpendiculares y la razón doble (A B M N) = -1, resulta que CM y CN son las bisectrices del ángulo ACB, y se verifica que . 

Con esto ya podemos ir a la resolución del problema.                                                   

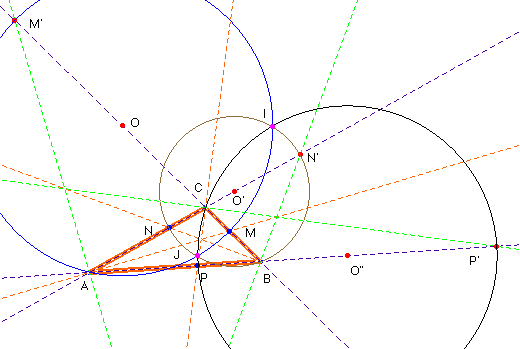         Construyamos las tres circunferencias de Apolonio. Vamos a dos demostrar que se cortan en únicamente dos puntos: los puntos isodinámicos, I y J. Supongamos que  I pertenece a las circunferencias de Apolonio del ángulo A y del ángulo B de centros los puntos O y O’ respectivamente.  Vamos a probar que también pertenece a la del ángulo C y centro O”. Según acabamos de ver la razón de las distancias de I a los vértices B y  C es constante e igual a . La razón de las distancias a C y a A también es constante: . Multiplicándolas entre sí se tiene: . (*)

Aplicando el teorema de Ceva a las tres bisectrices del triángulo obtenemos:

.   (**)  Combinando (*) y (**) obtenemos finalmente  que prueba la pertenencia del punto I a la circunferencia de Apolonio del ángulo C, como se quería demostrar. Con el punto J se procede exactamente igual.