Problema nº 20.- Triángulo semejante sobre semejantes.
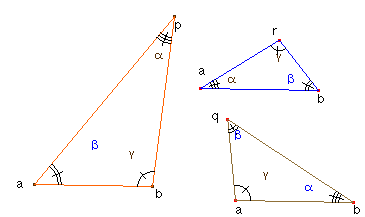
Dado un segmento ab y un triángulo arbitrario no equilátero jkm, construyamos sobre ab triángulos pab, bqa y abr semejantes a jkm. Entonces pqr es semejante a jkm.
Solución Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (4 de marzo de 2003)
Solución.-
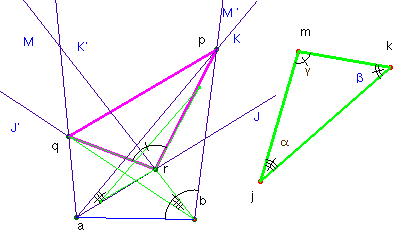
Las relaciones de semejanza entre los triángulos del enunciado nos llevan a las siguientes relaciones entre sus lados:
![]() (1);
(1);
![]() (2) y
(2) y
![]() (3)
(3)
En la figura se observa que los ángulos qbr y par son iguales (iguales a b-a). Veamos si son semejantes los triángulos respectivos. (Un giro de centro r y ángulo brq pone en evidencia la conjetura).
![]() por
(3);
por
(3);
![]() por (2)
y
por (2)
y
![]() por (1).
por (1).
De ahí se sigue que
![]() ,
,
o lo que es igual
, ![]()
y los triángulos son semejantes. Se tiene pues otra relación:
![]() (4)
(4)
De la semejanza de estos triángulos se sigue que tienen igual el ángulo en r, si a éstos les restamos el ángulo arq se obtiene g=bra = qrp. La igualdad de la primera y última de las razones de (4) demuestra que pqr es semejante a abr, pues tienen un ángulo igual y los lados que lo forman son proporcionales. (Se corresponden br con qr; ar con pr y ab con pq ) ,
![]() .
C.Q.D.
.
C.Q.D.