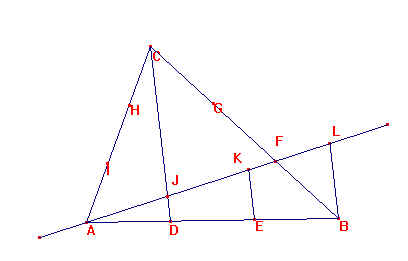
Sea ABC el triángulo.

Tomemos D, E sobre AB, F, G sobre BC y H, I sobre CA, que dividan a cada lado en tres partes iguales.

Tracemos la rectas AF, CD y por E y B sendas paralelas s y t a CD.

Llamemos:

J al punto de intersección de AF con CD;

K al punto de intersección de s con AF y

L al punto de intersección de t con AF.

Los triángulos AJD, AKE y ABL son semejantes de razón 2 y 3 respectivamente, luego:

KE = 2JD, LB = 3 JD.

Por otra parte, los triángulos LBF y JCB son semejantes de razón 2, por

ser CD paralela a LB y

ser FC = 2 FB.

Luego tenemos que CJ = 2 LB = 2(3 JD) = 6 JD.

 

Tracemos ahora la recta que pasa por BK.

Cortará en CD en un punto M.

Tracemos por A la recta r paralela a CD. BK cortará a r en AN.

Los triángulos BKE, BMD y BNA son semejantes de razón 2 y 3 respectivamente.

Por ello,

MD = 2(EK) = 2(2 JD)= 4 JD.

De donde MJ= MD-JD= 4 JD-JD= 3JD,

y CM = CJ - JM= 6 JD- 3JD = 3JD.

NA = 3 (EK) = 3 (2 JD) = 6 JD.

Sea H' el punto de corte del lado AC con la recta BK.

Los triángulos MCH' y NAH' son semejantes por ser CM paralela a NA.

Además, NA= 6 JD y CM= 3 JD, por lo que la razón de semejanza es 2.

Por ello, es AH' = 2 CH', al ser lados homólogos en la semejanza.

Es decir, H' coincide con H.

Por tanto, es CM = CJ= 3JD. Por analogía en la construcción, es:

BK= KM= 3 MH

AJ = JK = 3 KF.

Así, el área de MJK, si condideramos la base KF, es igual al área de MAJ,

considerando la base AJ.

De esta manera, podemos "construir" una descomposición

de ABC en siete triángulos siguientes, con el mismo área:

MJK, AMJ, ACM, CMK, CBK, BJK y BJA.

Luego, cqd el área de MJK es 1/7 del área de ABC