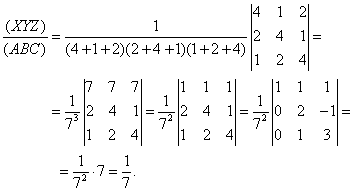
|
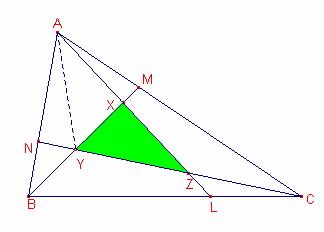
Los lados de un triángulo cualquiera se dividen en tres partes
iguales. Se une un vértice con uno de los puntos de división
del lado opuesto, y los otros dos vértices con los puntos homólogos
según la primera elección. De esta manera se forma un triángulo
interior al dado. Su área es 1/7 de la área del original. |
|
Propuesto por Francisco Anillo |
Solución de Francisco
Javier García Capitán
Usamos coordenadas baricéntricas:
 |
Del enunciado tenemos que 3L=2C+B, 3M=2A+C y 3N=2B+A. Entonces, 4A + 3L = 4A + 2C + B = 6M + B. Por tanto el punto X que está en las rectas AL y BM cumple 7X = 4A + B + 2C y sus coordenadas baricéntricas son (4:1:2). De forma similar tendremos:
Y (2:4:1), Z = (1:2:4).
Entonces el área del triángulo (XYZ) en relación al triángulo (ABC) viene dado por