16 de Marzo - 31 de Marzo de
2001 [Remitido por el profesor Francisco Anillo (Centro de Profesorado de
Córdoba)]
Problema
22.- Los lados de un triángulo cualquiera se dividen en tres partes iguales. Se
une un vértice con uno de los puntos de división del lado opuesto, y los otros
dos vértices con los puntos homólogos según la primera elección. De esta manera
se forma un triángulo interior al dado. Su área es 1/7 de la
área del original.
Oposiciones de Secundaria de
la Comunidad Autónoma Andaluza, 1.996
Gardiner , A. (1.987): Discovering
Mathematics. The Art of Investigation.
Jonhston, W.I. (Ed.)(1.992):
About the Cover Febrero. Mathematics Teacher
Kennedy, J(1.993): Drop the restriction, Marzo. Mathematics Teacher (p.192)
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.
.-
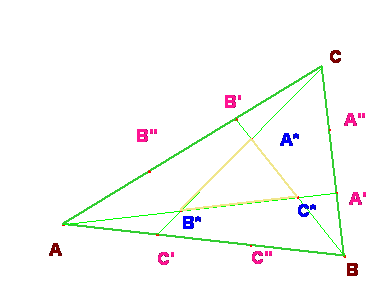
1.- Los triángulos ACC', ABA' y BCB' tienen, por
construcción, un área igual a un tercio de la de ABC. Por tanto su suma es la de éste. En esta suma aparecen dos
veces los triángulos de las esquinas,
esto es, AB*C', BC*A' y CA*B' y no se suma el triángulo
interior A*B*C*. Por consiguiente el
área de éste último es igual a la suma de las áreas de aquéllos.
2.- Aplicando el teorema de Menelao al
triángulo BCC' con AA' como transversal se obtiene (AC’B)·(A’BC)·(B*CC’)=1. Por la construcción realizada,
la primera razón simple vale 1/3, y la segunda -1/2, por tanto de la tercera se
obtiene, en valor absoluto, B*C= 6B*C'.
Con las transversales BB’ y CC’ en los triángulos AA’C y AB’B
respectivamente, obtengo de forma
similar: A*B= 6A*B' y C*A = 6 C*A'.
3.- De todo esto se deduce que el área de AC'C es 7 veces la de de AB*C' la de AA'B es 7 veces la de BC*A'
y la de B'BC
es también 7 veces la de CB'A*.
Como el área de cada
uno de estos tres triángulos es un tercio del total, deduzco que los tres triángulos
de las esquinas tienen igual área.
4.- De 1 tenemos Área (A*B*C*) = [A*B*C*]
= [ AB*C'] + [ BC*A'] + [ CA*B'] = 3[AB*C']= 3·1/7[AC'C] =1/7[ABC] como queríamos demostrar.
Generalización.
Si
dividimos los lados del triángulo en n
partes iguales, el razonamiento expresado en el punto 2 nos da en este caso (AC’B) = 1/n
y (A’BC)=
-
resultando por tanto, en valor absoluto, B*C= n(n-1)·B*C' , y por tanto las áreas de los
triángulos que antes eran 3·(3-1) +1 =7 veces las de los formados en las esquinas es ahora n(n-1)+1 veces mayor.
El área
total de ABC se obtienen sumando al
área del central, las áreas de los tres laterales AC’C,CB’B y BA’A (los tres de área igual a 1/n del total) y restando las áreas de las
tres esquinas.
Calculemos los términos
que intervienen:
[AB*C’]=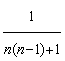
[AC’C]=
[ABC].
[A*B*C*]=[ABC]+3·[ AB*C’]-3/n·[ABC]=
[ABC]=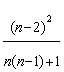
[ABC].
Para n=2 el área es cero: el triángulo
central se reduce al baricentro.
Para el valor 3 sale
1/7 que ya habíamos visto.
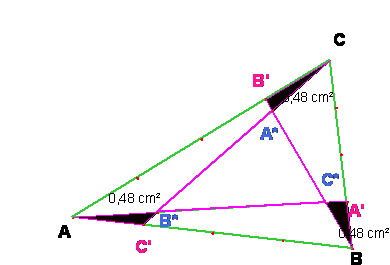
Para n=4, que es el mostrado en la segunda
figura, el valor del área del triángulo central es 4/13.
Se ve cómo al crecer n crece también el área de ese triángulo,
tendiendo a igualarse con ABC en el
infinito.