Problema 23
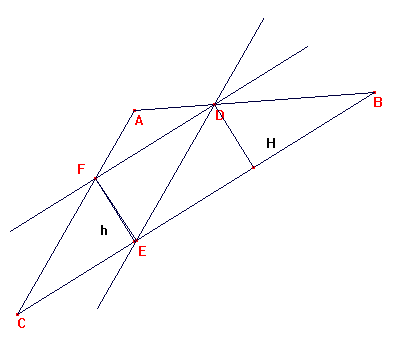
ABC es un triángulo cualquiera y D un punto del lado AB que divide a este en dos segmentos que están en proporción de 1 a 2. Si DE y DF son segmentos paralelos a los lados AC y BC, respectivamente, ¿qué relación hay entre las áreas de los triángulos DBE y FEC?
Solución del profesor Rogelio Jalón, del IES Arrabal de Carmona (España)

El triángulo DBE tiene un área que es doble que la del CFE.
Ambos triángulos tienen la misma altura, por ser la distancia entre dos rectas paralelas (H = h).
La base CE es la mitad que la EB, ya que por el Teorema de Thales, si AD es un tercio de AB
(por construcción), CE también es un tercio de CB, luego EB = 2 CE.
Si el triángulo DBE tiene la misma alura y el doble de base que el CFE tendrá el doble de área,
como queríamos demostrar.