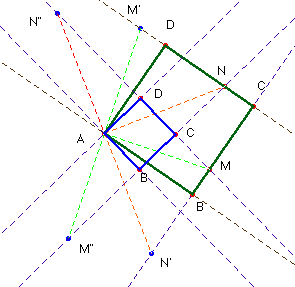
Problema nº 24.- Construir un cuadrado, si se conocen uno de sus vértices y dos puntos en los dos lados o sus continuaciones, que no pasan por el vértice dado.
Solución de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (4 de marzo de 2003)
Un giro de 90º de centro el vértice dado A lleva uno de los puntos M a M’; si el ángulo de giro es –90º lo lleva a la posición M”. La recta M’N contiene dos vértices del cuadrado, distintos de A. El resto es trivial. Análogamente con M”N.
Si tomamos N en vez de M, con los puntos N’ y N” obtenemos el mismo resultado.
Hay, pues dos soluciones al problema.