SOLUCIÓN AL PROBLEMA 26

Profesora Fabiola Czwienczek Müller

Universidad Pedagógica Experimental Libertador

Maracay, Venezuela

e-mail:fabiolacz44@hotmail.com

PROBLEMA

Si Z y X son centros de cuadrados construidos hacia el exterior sobre los lados de un triángulo ABC cualquiera y M es el punto medio del tercer lado, entonces ZMX es isósceles y tiene un ángulo recto en M.

SOLUCIÓN

Sea ABC un triángulo. Denotemos por Z al centro del cuadrado construido hacia el exterior sobre el lado AB y por X al centro del cuadrado construido hacia exterior sobre el lado AC. Sea M el punto medio del lado BC.

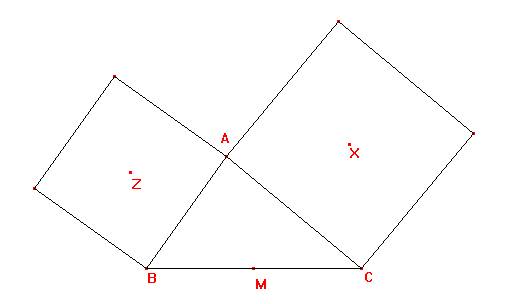
Por las condiciones del problema, se tiene que los ángulos BZA y CXA son rectos. Además, ZB = ZA y XC = XA.

Consideremos la rotación con centro en Z y ángulo de rotación de 90º en sentido positivo (antihorario). La imagen de Z es, obviamente Z, la de B es A y la de M la denotaremos por M´.

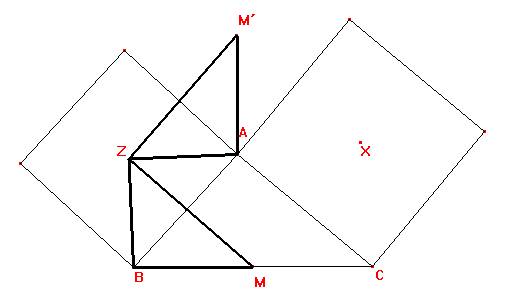
Los triángulos ZBM y ZAM´ son congruentes. Por tanto,

1) BM = AM´

2) ZM = ZM´.

Por otra parte, la recta determinada por los puntos A y M´ es la imagen de la recta determinada por los puntos B y M. Por propiedad de las rotaciones, estas rectas forman un ángulo de igual medida que el ángulo de rotación. En consecuencia, estas rectas son perpendiculares y tenemos que la recta AM´ es la perpendicular a la recta BM trazada desde A. Análogamente, los segmentos ZM y ZM´ son perpendiculares.

Consideremos, ahora, la rotación con centro en X y ángulo de rotación de 90º en sentido negativo (horario). La imagen de X es, obviamente X, la de C es A y la de M la denotaremos por M´´.

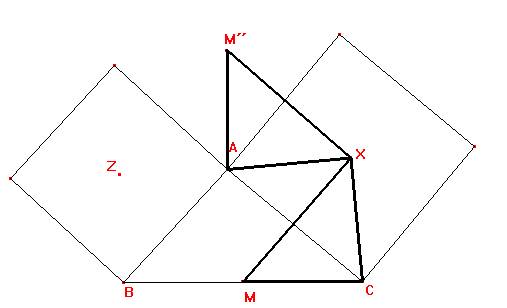
Los triángulos XCM y XAM´´ son congruentes. Por tanto,

3) CM = AM´´

4) XM = XM´´.

Por el mismo razonamiento aplicado anteriormente, podemos garantizar que la recta AM´´ es la perpendicular a la recta BM trazada desde A y que los segmentos XM y XM´´ son perpendiculares.

Probaremos que M´´= M´. Como desde un punto dado existe una única perpendicular a una recta dada, se tiene que las rectas AM´ y AM´´ son iguales. Así, los puntos A, M´ y M´´ están alineados. Por los sentidos tomados para efectuar las rotaciones, no es posible que el punto A esté entre M´ y M´´. Esto significa que M´´ pertenece a la semirrecta AM´. No olvidemos que M es el punto del medio del segmento BC, con lo cual BM = CM. De esta última igualdad y de las igualdades 1) y 3), se deduce que AM´= AM´´. Por tanto, M´´= M´.

Así, los puntos Z, M, X y M´ determinan un cuadrilátero en el cual:

- el ángulo en Z es recto

- el ángulo en X es recto

- ZM = ZM´

- XM = XM´

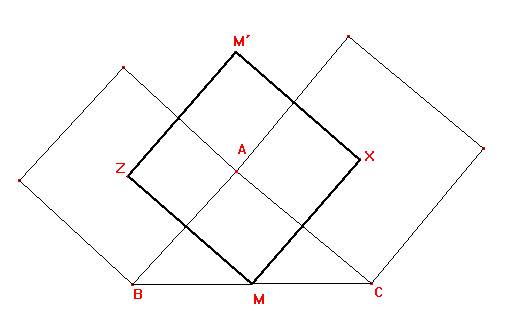
Con todas estas condiciones es fácil probar que el cuadrilátero ZMXM´ es un cuadrado. Se deduce, así, que ZMX es isósceles y tiene un ángulo recto en M, que era lo que queríamos demostrar.

Fabiola Czwienczek