SOLUCIÓN AL PROBLEMA 27

Profesora Fabiola Czwienczek Müller

Universidad Pedagógica Experimental Libertador

Maracay, Venezuela

e-mail:fabiolacz44@hotmail.com

PROBLEMA

Si construimos cuadrados sobre los lados de un triángulo hacia el exterior, entonces el segmento que une dos centros de dichos cuadrados es perpendicular y congruente al segmento que une al tercer centro con el vértice opuesto al mismo.

SOLUCIÓN

Sea ABC un triángulo. Sean Z, X y Y los centros de los cuadrados construidos hacia el exterior del triángulo ABC sobre los lados AB, AC y BC, respectivamente. Consideremos los segmentos ZX y AY; el primero une dos centros de dichos cuadrados y el segundo, el tercer centro con el vértice opuesto al mismo. Debemos probar que ZX y AY son perpendiculares y congruentes.

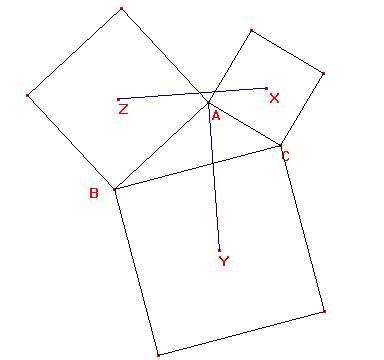
Sea M el punto medio del lado AC. Por el problema 26, sabemos que ZM y YM son segmentos congruentes y perpendiculares. Como X es el centro del cuadrado construido sobre AC, se tiene que AM = XM y que el ángulo XMA es recto. Consideremos la rotación con centro en M y ángulo de rotación de 90º en sentido positivo (antihorario). Luego, la imagen de M es M, la de Y es Z y la A es X.

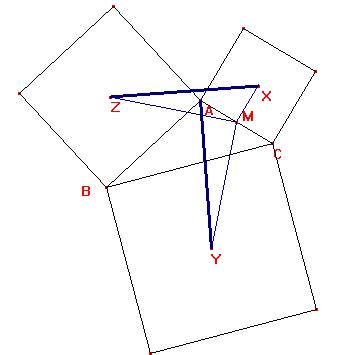
Nótese que los triángulos AMY y XMZ son congruentes. Por tanto, AY = XZ.

Por otra parte, la recta determinada por los puntos Z y X es la imagen, a través de la rotación de 90º en el sentido establecido, de la recta determinada por A y Y. En consecuencia, estas rectas son perpendiculares y, por ende, lo son también los segmentos ZX y AY. Q.E.D.

Fabiola Czwienczek