Solución del profesor de Matemáticas del IES Fray Luis de León de Salamanca Saturnino Campo Ruiz,

Problema nª 28.-

 

 

 

 

 

 

 

 

 

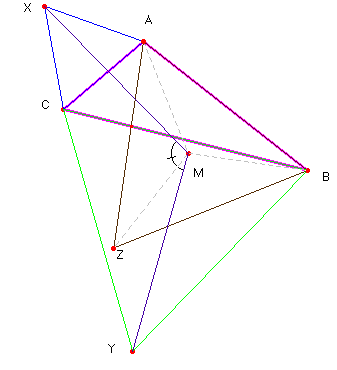
Colorario 3.- Supongamos que se construyen triángulos equiláteros sobre los lados de un triángulo arbitrario, dos hacia el exterior y uno hacia el interior. Sea M el centro del triángulo equilátero interior, y X e Y los vérti­ces exteriores de los otros dos. Entonces XMY es un triángulo isósceles, con un ángulo de 120º en el vértice M

Finney, R. L. (1.970): Dynamic proofs of euclidean theorems. En Mathematics Magazine, (Sep-Oct. pp177-185), p. 182

 

 

 

 

 

 

 

 

 

 

 

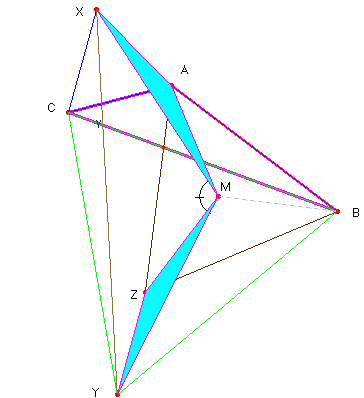
Solución.- Si hacemos un giro de centro B y amplitud 60º, el punto A se transforma en Z y el punto C se transforma en el Y. Por tanto el triángulo ABC se transforma en el trián­gulo BZX, donde el lado ZY = AC = AX. Otro giro de 120º y centro M, transforma el triángulo MAX en el MZY. De la igualdad de los ángulos que concurren en M, se concluye que el ángulo XMY es igual al ángulo que forman las bisectrices AM y ZM, es decir 120º.