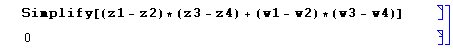PROBLEMA 29

Introducción

Si se unen cuatro puntos de un plano de dos en dos por medio de seis rectas distintas, se les llama vértices de un cuadrángulo completo y las rectas son sus seis lados.

    1.72 Si en un cuadrángulo completo hay dos pares de lados opuestos que son perpendiculares entre sí, los demás lados serán perpendiculares entre sí de la misma manera. Un cuadrángulo así, ABCH, se llama cuadrángulo ortocéntrico.

Ejercicios
4.- El incentro y los excentros de un triángulo cualquiera forman un cuadrángulo ortocéntrico.

Coxeter, HSM , (1.971) Fundamentos de Geometría.Limusa-Wiley. México Págs 42-43

Solución de Nicolás Rosillo. (26 de junio de 2003)

Dpto. Matemáticas, IES Máximo Laguna.

Santa Cruz de Mudela, Ciudad Real

nrosillo@olmo.pntic.mec.es

Sin pérdida de generalidad, se puede suponer una configuración como la siguiente:

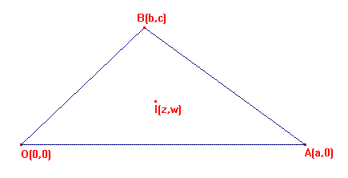
La circunferencia inscrita ha de ser tangente a los 3 lados del triángulo, por lo que en los puntos de intersección los radios han de ser perpendiculares a los lados, lo que indica que para la figura dada la longitud del radio es el valor absoluto de w. Así, una primera condición sobre (z,w) supuesto el incentro se obtiene escribiendo la ecuación de la circunferencia de centro (z,w) y radio w.

e imponiendo que un punto (x,y) de la misma esté en el lado OB:

a la que añadimos la condición para que el radio trazado en dicho punto sea perpendicular a ese lado:

Eliminado x e y en esas tres ecuaciones se obtiene la ecuación

como muestra la figura siguiente, describiendo parte de una sesión con Mathematica.

La ecuación obtenida relaciona (z,w) con las coordenadas de los vértices del triángulo.

Análogamente, haciendo lo mismo con el lado AB, se obtienen las ecuaciones

a partir de las cuales, por eliminación, se deduce una segunda condición de relación de las coordenadas del incentro:

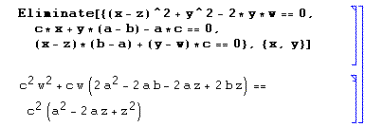
Resolviendo el sistema formado por las dos ecuaciones obtenidas, resultan las coordenadas de z y w en función de a, b y c:

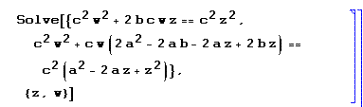
El programa obtiene las cuatro soluciones correspondientes, DE LAS QUE SÓLO SE MUESTRA UNA debido a su complejidad y tamaño:

Acto seguido, sólo queda calcular el producto escalar de dos vectores formados cada uno de ellos por dos distintas de las cuatro soluciones halladas.