Problema 3. 1-15 de novimbre de 2.000
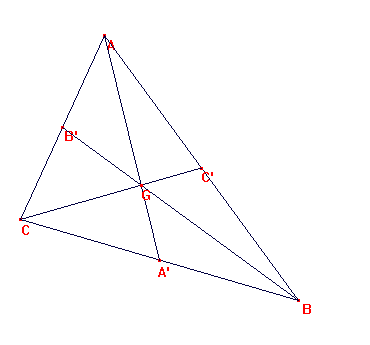
| mediana. Una mediana de un triángulo es una recta que pasa por un vértice y por el punto medio del lado opuesto. Las tres medianas se cortan en el centroide o baricentro. |

Sea ABC el triángulo y sean A', B' y C' los puntos medios de los lados.
Según el teorema de Ceva (ver el problema 37 de la página web), se cumple que
| Teorema de Ceva. Sean a, b c, los vértices de un triángulo y tres puntos a' de bc, b' de ca, y c' de ab sobre los lados de este triángulo. Entonces las tres rectas aa', bb', y cc' son concurrentes si y sólo si se tiene: (a'b / a'c) (b'c / b'a) (c'a/ c'b) = - 1 |
En este caso, por ser A'B = -A'C, B'C = B'A y C'A = -C'B,
se verfica la igualdad, y se tiene que deben cortarse en un punto.
Tal punto se denomina baricentro y es el centro de gravedad del triángulo
Ricardo Barroso Campos