Solución de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca) (20 de enero de 2003)
Problema nº 32.- Demostrar que en un la bisectriz interna de un ángulo y la mediatriz del lado opuesto se cortan sobre la circunferencia circunscrita.
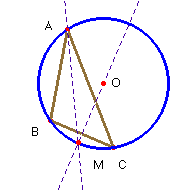
Solución.- La bisectriz del ángulo A nos proporciona dos ángulos iguales: el BAM y el MAC, por tanto también son iguales los arcos BM y MC. De ahí que los segmentos correspondientes, esto es, la distancia de M a B y la distancia de M a C sean iguales. Eso es igual que decir que M está en la bisectriz OM del lado AB.