5.- Demostrar que en un triángulo, el incentro un excentro y los dos vértices
que forman el lado correspondiente al excentro son concíclicos y el centro de
esta circunferencia está sobre la circunferencia circunscrita. Martha Iglesias.
Anexo D-8. Tesis de maestría. Sección de problemas nº 2. pág 170
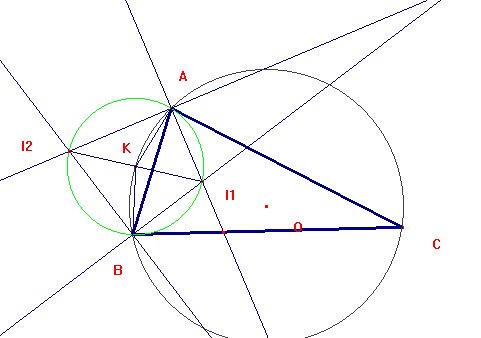
Dado el triángulo ABC, llamaremos I1 al incentro e I2 al exincentro correspondiente
a los vértices A y B. Los puntos I1, A, I2 y B están sobre una circunferencia
de diámetro I2I1 debido a que los ángulos
El ángulo AKB
= 2*(90º - C/2)= 180º - C. Es decir
Solución de Carlos Fleitas "IES Marqués de Santilana", Colmenar Viejo (Madrid)