124 Recta de Euler: Demostrar que en un triángulo arbitrario, el punto
de intersección de las alturas, el punto de intersección de
las medianas y el centro de la circunferencia circunscrita, están situados
en una recta. Esta recta se llama recta de Euler.
Solución de la alumna Maite Peña Alcaraz, del Colegio Porta Celi de Sevilla
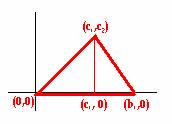
Si colocamos de esa manera en los ejes cartesianos un triángulo cualquiera y averiguamos su baricentro, su circuncentro y su ortocentro.
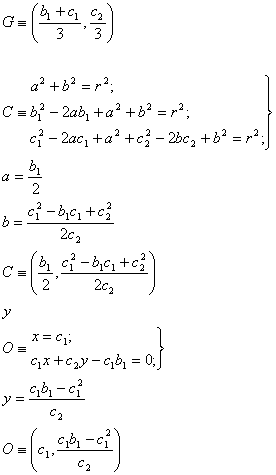
Y para ver si están alineados simplemente hay que ver si se cumple:
![]()
Entonces si lo aplicamos obtenemos:

Lo que es evidente que se cumple, luego está demostrado que el baricentro G, el circuncentro C y el ortocentro O, de un triángulo cualquiera están alineados.