Problema nº 7.-124 Recta de Euler: Demostrar que en un triángulo arbitrario, el punto de intersección de las alturas, el punto de intersección de las medianas y el centro de la circunferencia circunscrita, están situados en una recta. Esta recta se llama recta de Euler.
Solución.-
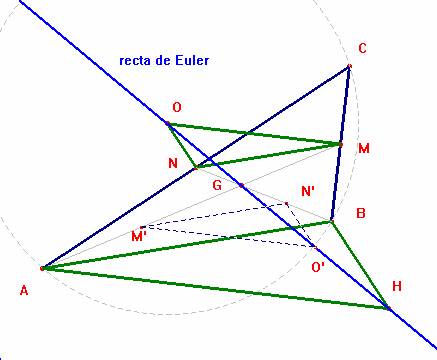 Sea OMN el triángulo formado por el circuncentro O y los puntos
medios M y N de los lados a y b. Este triángulo
es homotético al triángulo BAH formado con el punto H de intersección
de las alturas, por el paralelismo de sus lados. La correspondencia entre
puntos homólogos es M àA, N àB, O àH. El centro de la homotecia es el punto G de corte de
BN con AM, el baricentro del triángulo. Los puntos homólogos
O y H están alineados con el centro G de la homotecia.
Además los puntos M’ y N’ simétricos de M y N respecto
de G, según la propiedad de las medianas son los puntos medios de los
segmentos AM y BN, en consecuencia, O’ simétrico de O
respecto a G es el punto medio de GH. En conclusión: el
baricentro de un triángulo está alineado con el ortocentro y el circuncentro
y a doble distancia del primero que del segundo. La recta que contiene a estos
puntos se llama recta de Euler.
Sea OMN el triángulo formado por el circuncentro O y los puntos
medios M y N de los lados a y b. Este triángulo
es homotético al triángulo BAH formado con el punto H de intersección
de las alturas, por el paralelismo de sus lados. La correspondencia entre
puntos homólogos es M àA, N àB, O àH. El centro de la homotecia es el punto G de corte de
BN con AM, el baricentro del triángulo. Los puntos homólogos
O y H están alineados con el centro G de la homotecia.
Además los puntos M’ y N’ simétricos de M y N respecto
de G, según la propiedad de las medianas son los puntos medios de los
segmentos AM y BN, en consecuencia, O’ simétrico de O
respecto a G es el punto medio de GH. En conclusión: el
baricentro de un triángulo está alineado con el ortocentro y el circuncentro
y a doble distancia del primero que del segundo. La recta que contiene a estos
puntos se llama recta de Euler.