Problema nº 8.-
125. Circunferencia de Euler: Demostrar que en un triángulo arbitrario, las bases de las medianas, las bases de las alturas, y también los puntos medios de los segmentos que unen el punto de intersección de las alturas del triángulo con sus vértices, están situados en una circunferencia. Esta maravillosa circunferencia se llama a veces circunferencia de Euler.
Nesterensko, Yu. V., Olejnik, S.N. y Potápov, M.K. (1.994): Antiguos Problemas Recreativos en Rusia. Servicio Editorial Universidad Del País Vasco. (pag 85) (Traducción de Elena Aparicio Cortés, revisada por Emiliano Aparico Bernardo).
Solución del profesor Saturnino Campo Ruiz del IES Fray Luis de León (salamanca) (2 de Junio de 2003)
La demostración de esta extraordinaria propiedad se basa en otra, que, en
principio, se presenta como mucho más modesta y es la siguiente:
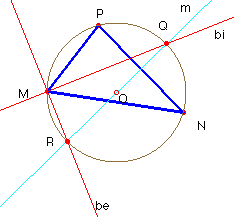
La circunferencia circunscrita a un triángulo contiene los puntos de intersección de la mediatriz de cada lado con las bisectrices del ángulo opuesto.
Demostrada esta propiedad tendremos, que esta circunferencia contiene, además de los vértices del triángulo, los seis puntos de intersección de las mediatrices de los lados con cada par de bisectrices del ángulo opuesto.
Ya está parcialmente demostrado en el problema nº 32, pero veámoslo completo ahora: Sean Q y R los puntos de corte de las bisectrices interior y exterior de M con la circunferencia circunscrita al triángulo MNP. Como los arcos NP y PQ son iguales, Q equidista de P y de N, por tanto, está en la mediatriz m del lado NP.
Por ser be la bisectriz exterior de M, el ángulo QMR es recto, y por consiguiente, RQ es un diámetro: la mediatriz del lado NP, pues cualquier mediatriz es un diámetro de la circunferencia circunscrita.
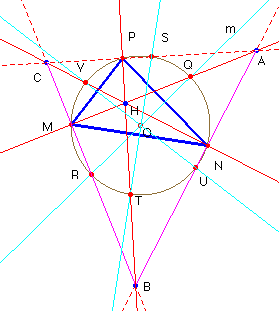Sea ahora MNP el triángulo órtico de un triángulo ABC. Las bisectrices
del triángulo órtico MNP son las alturas del triángulo ABC (Problema
nº 17).
Las alturas CN y BP determinan que los puntos H, P, A y N estén sobre una circunferencia de diámetro HA (son rectos los ángulos en P y en N); su centro ha de estar en el punto de este diámetro que también pertenece a la mediatriz m de NP, es decir, su centro es Q, así pues Q es el punto medio del segmento de la altura de A comprendido entre el ortocentro H y el vértice A.