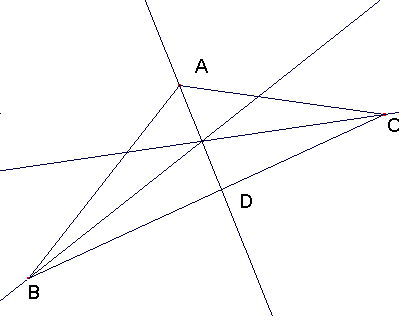
Problema 9.
| E32.- Demostrar que si en un triángulo un ángulo es de120º,
el triángulo formado por los pies de las bisectrices es rectángulo
|
Sánchez, G. (1.996): Métodos gráficos de resolución de problemas geométricos (pág 16) SAEM Thales. Sevilla.
Solución.
Este hermoso problema fue publicado por el profesor D. Gonzalo Sánchez Vázquez en 1.996
en un libro que recogía documentos de cursos sobre geometría impartidos a profesores de
Sevilla y Córdoba.
La solución que me facilitó D. Gonzalo (que fue fundador y presidente tanto de Thales (Sociedad Andaluza de Educación Matemática) como de la Federación Española de Sociedades de Profesores de Matemáticas es:

Sea ABC el triánguo con ángulo de 120º en A.
Consideremos el triángulo ABD formado por los vértices A, B del mismo y D el pie de la bisectriz del ángulo A.
Si considermos prolongado BA en BAM, AC es bisectriz externa de ABD en A, puesto que

BAC = 120º, BAD = 60º por ser AD bisectriz de BAC; Luego DAC = 60º y DAC = CAM = 60º.
Así pues el punto E pertenece a las bisextrices interna de ABD y externa por el ángulo A de ABD.
Luego E es un exincentro del triángulo ABD y DE es bisectriz externa de ABD en el ángulo D.

Por el mismo motivo, considerando el triángulo ACD, es DF bisectriz externa de ACD.
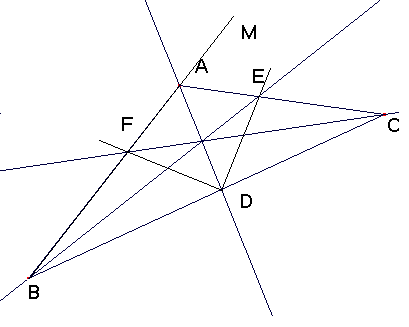
Tenemos que ADC + ADB = 180, Luego la suma de los ángulos fomados por sus bisectrices será:
EDA + EDA =90, cqd.
El profesor D. Gonzalo Sánchez Vázquez (1.917-1.996) fue un excelente matemático.