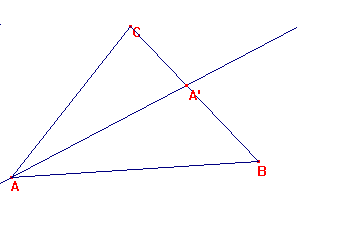
Solución del problema 6.-
| incentro. El incentro de un triángulo es el centro de la circunferencia inscrita. Es el punto en el que coinciden las tres bisectrices interiores de los ángulos del triángulo. |
Clapham, C. (1.992): Diccionario Oxford de Matemáticas. Celeste Ediciones. Madrid.
(Traducción de Alfonso Carlos Casal Piga y José Manuel Vegas Montaner)

Sea ABC un triángulo y sea AD la bisectriz del ángulo BAC.
Por el problema 1 de esta página WEB, tenemos que:
| 192. Teorema: En todo triángulo, la bisectriz de un ángulo interior divide al lado opuesto en dos segmentos aditivos directamente proporcionales a los lados de dicho ángulo. |
Bruño (1.950): Tratado de Geometría. Bruño. Madrid
De donde se tiene: A'B/A'C= AB/AC.

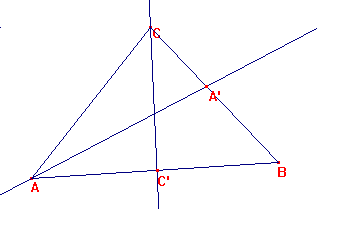
De igual manera, se tiene, C'A/C`B = CA/CB
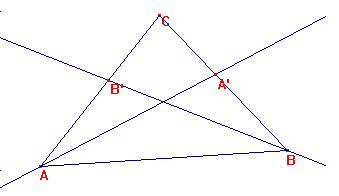
y, por otra parte, B'C/B'A= BC/BA.
Por ello, teniendo en cuenta el problema 37 de esta página WEB,
| Teorema de Ceva. Sean a, b c, los vértices de un triángulo y tres puntos a' de bc, b' de ca, y c' de ab sobre los lados de este triángulo. Entonces las tres rectas aa', bb', y cc' son concurrentes si y sólo si se tiene: a'b / a'c b'c / b'a c'a/ c'b = - 1 |
se tiene : (A'B/A'C)(B'C/B'A)(C'A/C'B)= (AB/AC) (BC/BA) (CA/CB)=-1, C.Q.D.
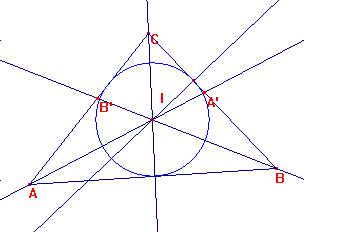
Es decir, existe un punto común a AA', BB' y CC', que llamaremos I.
Dada la propiedad de la bisectriz de que sus puntos están a la misma distancia de las dos rectas,
I está situado a la misma distancia de las tres rectas AB, BC y CA, por lo que es el centro de la
circunferencia inscrita.
Ricardo Barroso