Profesora Fabiola Czwienczek Müller
Universidad Pedagógica Experimental Libertador
Maracay, Venezuela
e-mail:fabiolacz@hotmail.com
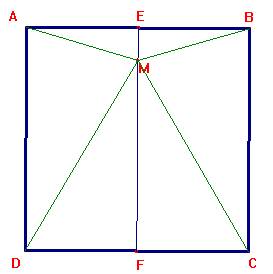
PROBLEMADesde los vértices A y B de un cuadrado ABCD se trazan en el interior del cuadrado unas líneas rectas que forman ángulos de 15º con AB. Estas dos rectas se cortan en M. Demostrar que el triángulo DCM es equilátero. |
Consideremos el cuadrado ABCD. Sean E y F los puntos medios de AB y DC, respectivamente. La mediatriz de AB, que coincide con la de DC, contiene al segmento EF. Sea M un punto cualquiera de EF . Se tiene que
AM = MB y DM = MC
Además, m < EAM = m < EBM y m < FDM = m < FCM (ver figura)
Hagamos AB = a y EM = h. Luego, MF = a – h . Nótese que la suma de las áreas de los triángulos AMB y DMC es la mitad del área del cuadrado ABCD. Esto es,
Por otra parte,
tan < EAM = 2h/a y tan < FDM = 2(a – h )/a
Sustituyendo en (1), se obtiene:
Simplificando, tenemos que
tan < EAM + tan < FDM = 2
En el caso del problema que nos ocupa, m < EAM
= 15º. Se puede determinar fácilmente que tan 15º = 2 – 
. aplicando la fórmula para calcular
tan (a - b), siendo a = 45º y b
= 30º. Luego,
tan < FDM = 2 – tan
15º = 2 – ( 2 – 
) = 
Así, m < FDM = m < FCM = 60º. Se concluye, entonces, que el triángulo DCM es equilátero. QED
Fabiola Czwienczek