|
Demostración de la fórmula de Herón: El área de un triángulo de lados a, b y c, y semiperímetro s es:
|
|
Demostración de la fórmula de Herón: El área de un triángulo de lados a, b y c, y semiperímetro s es:
|
Heat, T. (1.921/1.981) A history of Greek Mathematics. Dover Publications; Inc. New York.
Sea el triángulo ABC y sus lados de longitudes a,b,c.
Inscribamos el círculo DEF y sea O el centro, con
OD, OE y OF perpendiculares a BC, CA, y AB.
Tenemos: BC* OD= 2 D BOC, CA* OE= 2 D COA, AB* OF= 2 D AOB
Y, sumando, es: p* OD= 2 D ABC, por ser OD=OE=OF y siendo p el perímetro.
Tomemos sobre CB el punto H tal que BH = AF.
Entonces, siendo AE=AF, BF =BD y CE=CD, tenemos que: CH = 1/2 p = s.
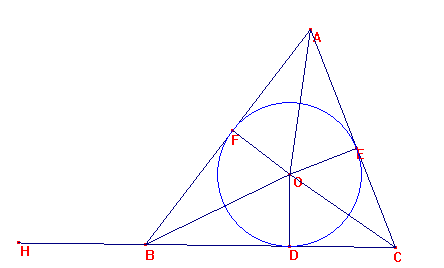
Siendo, pues, CH * OD = D ABC., y por ello, es : (D ABC)2 = CH2 * OD2
Tomemos OL de manera que forme ángulo recto con OC y que BL forme
ángulo recto con a BC . OL cortará a BC en K .Unamos C con L.
Tenemos que dado que COL y CBL son rectos, el cuadrilátero COBL está inscrito
en una circunferencia.
Por ello, Pero Luego los ángulos COB y AOF juntos son iguales a los AOC y BOF, siendo la suma de los 4 ángulos 4R. Por tanto, de [1] y [2], se tiene que Luego los triángulos rectángulos AOF y CLB son semejantes. Considerando que BKL y KDO también son semejantes, tenemos que : De aquí, se tiene que: Así pues, (D
ABC)= CH 2 OD 2 = CH* HB* BD* DC = s(s-a)(s-b)(s-c).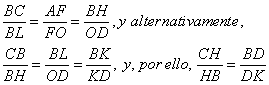 
, dado que el triángulo COK es rectángulo.
