Nota del editor
Involución ortogonal de un triángulo.
Sea ABC el triángulo dado.

Por B tracemos las perpendiculares a BC y a BA, y prolonguemos AC.

La circunferencia circunscrita a BDE es la involución ortogonal de ABC de centro B
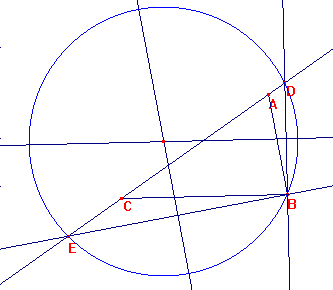
A continuación los puntos F y F' se toman sobre esa circunferencia de manera que son la intersección de la misma con la recta que pasa por los pies de las alturas de A sobre BC, L y de C sobre AB, M.
La misma construcción se hace respecto a los tres vértices.
Ricardo Barroso