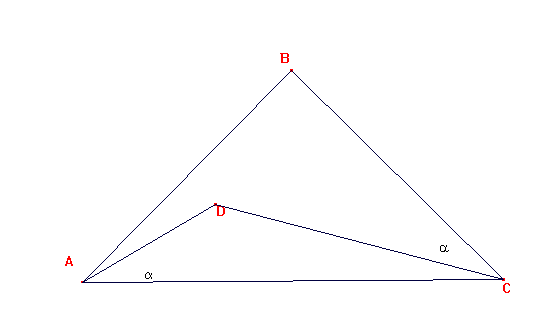
Solución del problema 48

Sea ABC un triángulo rectángulo en B e isósceles.
Sea D un punto interior del triángulo ABC tal que

CD = CB = BA, y tal que a = < DCB = < DAC

Calcular a.

Julio A. Miranda Ubaldo

Academia San Isidro (Huaral), de Perú

jmiub@yahoo.com

Soluación:

Tenemos la siguiiente figura:

Si trazamos el triángulo equilátero ACE de manera que tenga en su interior a ABC, tenemos:

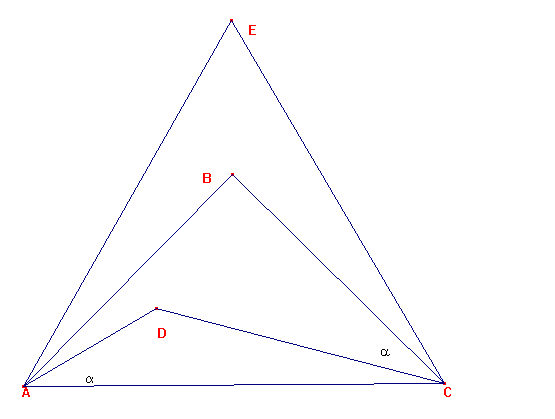
De acuerdo con la figura,:

ABC, < BAD= < DCA = 45º- a

< ADC = 135º.

AE=CE=AC.

Luego: < EAB= < ECB = 15º.

Uniendo E con B, el triángulo EAB es semejante al ECB

Por ello, < AEB = < BEC = 30º. < EBA= 135º.

En la figura los triángulos AEB y ADC son semejantes.

Por ello, a = 30º.