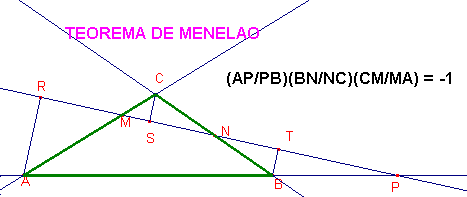
Una condición necesaria y suficiente para que tres puntos M, N y P situados sobre los lados de un triángulo estén alineados es que se cumpla la condición: (AP/PB)(BN/NC)(CM/MA) = -1

A) Veamos que es necesaria:
Consideremos las proyecciones (R, S y T) de los vértices del triángulo sobre la recta determinada por los puntos M, N y P. Los triángulos AMR y MCS, por un lado, los NCS y NBT por otro, y los APR y BPT por otro, son semejantes. De las semejanzas indicadas se deduce: AR/BT = AP/BP y BT/CS = BN/CN y CS/AR = CM/MA. Multiplicando miembro a miembro las tres igualdades obtenemos 1 = (AP/PB)(BN/CN)(CM/MA). Reescribimos el segundo miembro de la igualdad del siguiente modo: (AP/PB)(BN/NC)(CM/MA) y, teniendo en cuenta que la recta tiene que cortar al triángulo en uno o en tres puntos exterioriores a sus lados, resulta que la igualdad anterior toma el valor 1 pero con signo negativo si consideramos los segmentos con orientación.
B) La condición es necesaria:
Supongamos que se cumple la condición anterior y que los puntos M, N y P no están alineados. Consideremos la recta determinada por M y N y llamemos P' al punto de intersección de esa recta con el lado determinado por los vértices A y B.
Por hipótesis tenemos: (AP/PB)(BN/NC)(CM/NA) = -1, y por el resultado A) sabemos que se tiene que cumplir: (AP'/P'B)(BN/NC)(CM/NA) = -1.
De ambas igualdades se obtiene AP/PB = AP'/P'B y, teniendo en cuenta que en esta situación P y P' son ambos o bien interiores o bien exteriores simultáneamente al segmento AB (dependiendo del signo de las relaciones anteriores), se deduce que los puntos P y P' coinciden lo que contradice la hipótesis de partida.
El applet siguiente permite ver la situación del teorema de Menelao. Se puede deformar el triángulo actuando sobre sus vértices y se puede modificar la recta desplazando los puntos M y N