Problema 50. 1-15 de abril de 2002
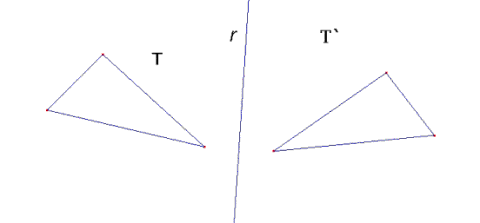
| Demostrar
que dando sólo dos «cortes rectos» a cualquier triángulo
T, y dada cualquier recta r, se puede descomponer en tres figuras geométricas
(dos triángulos y un cuadrilátero) que pueden ser «reagrupadas»
usando sólo rotaciones y traslaciones (no simetrías) construyendo
T’ (triángulos simétrico de T respecto a r). |

Klee,
V. Y Wagon, S. (1991): Old and new unsolved problems in Plane Geometry and Number
Theory, MAA Dolocian Mathematical Expositions, nº 11 (pág 52).