Solución de Ramón Trigueros Reina; IES Miguel de Mañara de San José de la Rinconada y Profesor Asociado del Dpto. de Didáctica de las Matemáticas, Universidad de Sevilla

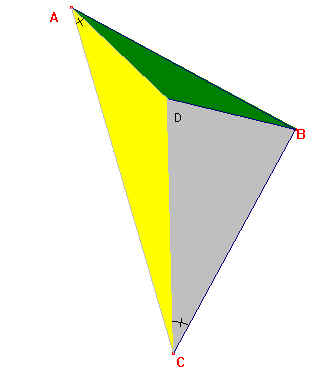
Sea ABC un triángulo rectángulo en B e isósceles

Sea D un punto interior del triángulo ABC tal que

CD=CB=BA, y tal que   a = < DCB = < DAC

Calcular a

El área del triángulo ABC es la suma de las áreas de los triángulos CBD, CDA y ADB.

Si llamamos el lado AB = L nos queda área del triágulo ABC = ( L²)/2

El área del triángulo BCD = ( L²)sen a /2 ;

Por otra parte esa misma área se pude calcular utilizando los lados AD y AC quedando

De donde

y por tanto

Desarrollando y simplificando, resulta:

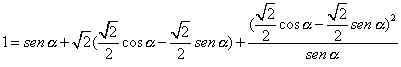
y de aquí,

por lo que