Problema 37:

Teorema de Ceva. Sean a, b c, los vértices de un triángulo y tres puntos a' de bc, b' de ca, y c' de ab sobre los lados de este triángulo. Entonces las tres rectas aa', bb', y cc' son concurrentes si y sólo si se tiene:

a'b / a'c b'c / b'a c'a/ c'b = - 1

Berger, M (1.990). Géomètrie. Nathan. LUÇON

Demostrar el Teorema de Ceva:

Solución de Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid) (8 de noviembre de 2004)

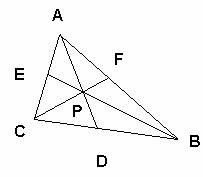
Sabemos que el área de CPA/APB=CD/DB (Porque CPA y APB son respectivamente CAD-CPD y DAB-DPB cuyo cociente es CD/DB porque tienen las misma alturas y bases CD y DB respectivamente)

Igualmente, BPC/CPA=BF/FA y APB/BPC=AE/EC, y si multiplicamos estas expresiones obtenemos CD BF AE / (DB FA EC)=1, por lo que queda demostrado.

Probar que si BD * CE * AF = DC * EA * FB, siendo AD, BE y CF tres cevianas del triángulo ABC, entonces AD, BE y CF son concurrentes.

Supongamos que no. Entonces BE cortará a AD en el punto P y CF cortará a AD en el punto Q.

Si unimos CP y llamamos F´ al punto en que interseca a AB, por el Teorema de Ceva tenemos que BD*CE*AF´=DC*EA*F´B, y dividiendo por la otra expresión obtenemos que AF/FB=AF´/F´B y por tanto F´ºF, ya que solo existe un punto en un segmento que lo divide en una razón dada.

Así que si se cumple la primera igualdad sin que las cevianas sean concurrentes, como F´ºF, PºQ en contra de lo que habíamos supuesto. Contradicción y hemos acabado.