Una cúbica circular en la que se contienen algunos puntos notables del triángulo

Por

François Rideau, Maitre de Conférences à l'Université de Paris 7 (Traducción libre: Ricardo Barroso),

3 La utilización de las coordenadas baricéntricas.

En esta sección se dejan completamente los números complejos y se interesa en buscar una ecuación del lugar en coordenadas baricéntricas con relación al triángulo ABC. Precisemos bien la situación:

- en primer lugar las notaciones: las letras a, b, c designan ahora las longitudes de los lados del triángulo ABC:

a = BC; b=CA; c=AB.

- para todo el punto M del plano, existe una tripleta (x, y, z) R³; x+y+z 0 definiendo un escalar multiplicativo no nulo tal que siendo M el baricentro los puntos de masas (A,x), (B,y), (C,z); se dice que el trío (x, y, z) forma un sistema de coordenadas homogéneas del M. Cuando la suma de las masas es igual a 1, (x+y+z=1), se dice que la tripleta (x, y, z) forma el sistema de coordenadas baricéntricas de M en la referencia afín (A, B, C). La tripleta de las coordenadas baricéntricas de M se define de manera única y se tiene para todo el punto O del plano:

OM=xOA+yOB+zOC

y se escribe: M=x A+y B+z C.

lo que equivale a identificar todo punto M del plano con la función vectorial elemental de Leibniz O → OM .

Las funciones vectoriales de Leibniz forman un espacio vectorial llamado prolongado vectorial de P.

- la teoría vectorial prolongada permite pues dar sentido a las sumas x A+y B+z C incluso cuando x+y+z ≠ 1. Sin volver a entrar en detalles, este vectorial prolongado en el cual tienen sentido las sumas x A+y B+z C forma un espacio vectorial de dimensión 3 sobre R del que la tripleta в = (A, B, C) es precisamente una base.

- Este vectorial prolongado contiene pues el plano P como plano afin de ecuación x+y+z=1 en la base в. Contiene también el plano vectorial de ecuación x+y+z=0 en la base в. Este plano se identifica de manera natural con el espacio de los vectores observando que si x+y+z=0, la función vectorial de Leibniz O→xOA+yOB+zOC es constante. Es decir, existe un vector tal que:

V=xOA+yOB+zOC;

Y se escribe: V=xA +yB+zC

Se dice que la tripleta (x, y, z) forma el sistema de componentes baricéntricas de V en la base в.

El plano de los vectores se identifica así de manera natural con las funciones vectoriales de Leibniz que son constantes.

Si M=x A + y B + z C y M' =x' A + y' B + z' C son 2 puntos de P de coordenadas baricéntricas respectivas (x, y, z) y

(x', y', z'), entonces:

MM'= (x'-x)A+(y'-y)B+(z'-z)C

Las componentes baricéntricas del vector MM' son simplemente:

(x'-x, y'-y, z'-z)

-en esta base B, el cuadrado escalar del vector V=x A + y B + z C está dado por la ecuación:

(9)

y por lo tanto el producto escalar de los vectores V=x A + y B + z C y W=x' A + y' B + z' C está dado por la fórmula:

(10)

- va a ser necesario calcular ahora las expresiones que dan las simetrías con relación a los lados en coordenadas baricéntricas. Si se recuerda que estas simetrías ortogonales son también afines, ello resultará del lema siguiente fundamental en Geometría afin:

Se sabe que una aplicación afin f del plano P viene completamente determinada por las imágenes f (A), f (B), f (C).

En la referencia afin (A, B, C), es llaman:

- (a₁₁, a₂₁, a₃₁) las coordenadas baricéntricas de f (A)

- (a₁₂, a₂₂, a₃₂) las coordenadas baricéntricas de f (B),

- (a₁₃, a₂₃, a₃₃) las coordenadas baricéntricas de f (C),

- X= (x, y, z) las coordenadas baricéntricas de P

- X'= (x', y', z') las coordenadas baricéntricas de P'=f (P)

Lema 4 entonces X'=M. X donde:

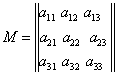
¡Eso se asemeja furiosamente a la matriz de una aplicación lineal aparte del hecho de que a priori M se limita a las tripletas (x, y, z) tales que x+y+z=1 que solo tienen el derecho consagrado a representar las coordenadas baricéntricas de los puntos del plano Allí interviene lo vectorial prolongado: la aplicación afin f se prolonga naturalmente de manera única en un endomorfismo vectorial prolongado y la matriz M es precisamente la matriz de en la base в= (A, B, C).

Tenemos ahora suficiente material para atacar el problema propiamente dicho.

La matriz de la simetría con relación a BC está pues de la forma:

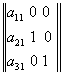
donde (a₁₁, a₂₁ ,a₃₁) son las coordenadas baricéntricas del punto L simétrico de A con relación a BC.

Las coordenadas baricéntricas del punto medio de AL son pues:

Como este punto debe situarse sobre BC, se tiene pues, que :

a₁₁= -1

Es necesario escribir ahora que el producto escalar de los vectores AL de componentes baricéntricas (-2, a₂₁ a₃₁) y BC de componentes baricéntricas (0, -1, 1) es nulo. Habida cuenta de la fórmula (10), se obtiene:

Se obtiene entonces el sistema siguiente:

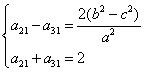
Cuya solución es:

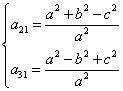
Las fórmulas que dan las coordenadas baricéntricas (x', y', z') del punto A' en función de las coordenadas baricéntricas

(x, y, z) del punto M son pues:

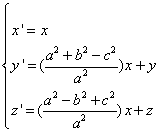
Se desprende inmediatamente que la ecuación de la recta AA' en coordenadas baricéntricas es:

Se obtiene sin cálculos, mediante permutaciones circulares: a→b→c→a, x→y→z→x ,X→Y→Z→X, las ecuaciones de las rectas BB' y CC'. Estas rectas serán pues convergentes si el sistema siguiente es compatible

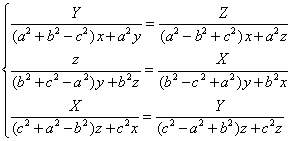
Lo que se traduce en la fórmula siguiente que es la ecuación en coordenadas u homogéneas del lugar buscado:

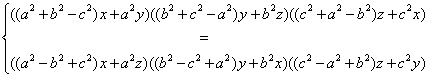
Bajo esta forma, se comprueba fácilmente que los centros de los círculos inscrito y exinscritos forman parte del lugar ya que sus coordenadas homogéneas son de la forma (±a, ±b, ±c). Me detengo allí sobre este tema, mi único interés será poner de manifiesto que se podía formar la ecuación de este lugar en coordenadas baricéntricas pero puede obviamente servirme para responder a otras cuestiones sobre este cúbica.

Continúa en casos particulares (isósceles, equilátero)