Problema nº 45.- Teorema de Menelao
(sobre 70-130 d. C)
Si tres líneas formando un triángulo se cortan por una transversal, el
producto de las longitudes de los tres segmentos que
tienen extremidades no comunes es igual al producto de las otras tres.
Smith, D.E. (1.923/1958)
History of mathematics.
Solución de Solución de Saturnino Campo Ruiz, profesor del IES
Fray Luis de León, de
Salamanca (29 de marzo de 2006).-
Concretando, si se tiene una transversal que corta a los lados de un triángulo en puntos A’, B’ y C’ el producto de las razones simples (A’BC), (B’CA) y (C’AB) es igual a la unidad. (La razón simple de tres puntos alineados M, N y P es (MNP)=MN/MP).
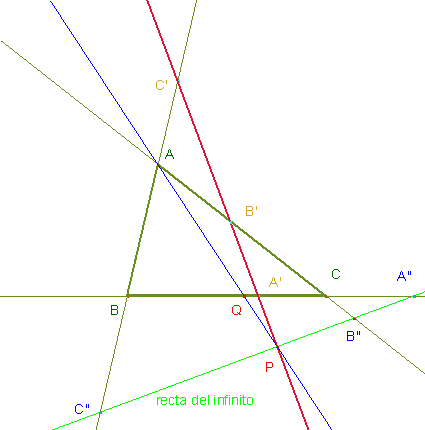
Supongamos que la recta del
infinito corta a los lados del triángulo (o a sus prolongaciones) en los puntos
A”, B” y C”. Entonces, la
razón simple (C’AB) es igual a la
razón doble (C’C”AB). También (B’CA)=(B’B”CA).
Sea P el punto del infinito de la transversal; proyectando desde P sobre el lado BC, (C’C”AB)
= (A’A”QB) = (A’QB) y (B’B”CA) = (A’A”CQ) = (A’CQ).
El producto de las tres razones
simples es pues (B’CA)·(C’AB)·(A’BC) = (A’CQ)· (A’QB)·
(A’BC) =(A’CB)·(A’BC) = +1. c.q.d.