Solución del problema 47.
Profesor Julio A. Miranda Ubaldo, de la Academia San Isidro (Huaral), de Perú.
jumiub@yahoo.com
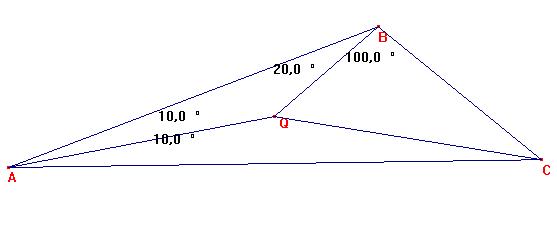
Sea un triángulo ABC. Sea Q punto interior del triángulo ABC, de manera que tenemos:
< QAB = < CAQ=10º , < ABQ=20, <QBC= 100º. Calcular <ACQ.

De acuerdo con la figura, tracemos la ceviana BM de modo tal que < QMB= 60º y <MBC=40º:
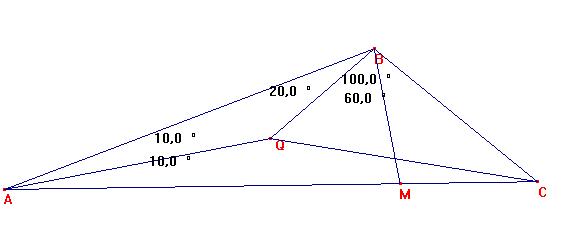
Es < BCA = 180º -10º -10º -20º -100º = 40º por las condiciones del problema.
Es < MBC= 40º por la construcción hecha.
Luego MBC es isósceles ( BM = MC).
Por otra parte, < ABM = < AMB =80º, por lo que el triángulo MAB es isósceles, y AM=AB.
Uniendo Q con M, los triángulos BAQ y MAQ son semejantes pues tienen dos lados comunes (el AQ) dos lados iguales (AM y AB) y el ángulo comprendido < BAQ y <MAQ de la misma medida.
Luego < QMA = 20º, y < BMQ = 60º.
Así, el triángulo BMQ es equilátero, y BM= MQ= QB.
Luego el triángulo QMC es isósceles, puesto que MC = BM = MQ.
Es < QMC= 180 - < QMA = 160º.
Y, 2 < QCA = 180 - < QMC = 20º.
De donde se tiene que < QCA= 10º.