Laboratorio virtual de triángulos con Cabri.
Problema nº 48: Solucíón de Enrique de la Torre Fernández (Universidad de A Coruña
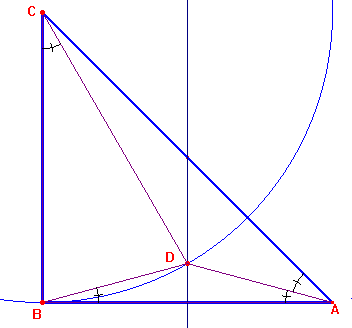
Sea ABC un triángulo rectángulo en B e isósceles.
Sea D un punto interior del triángulo ABC tal que CD=CB=BA, y tal que
Demostración:
(Lo que se quiere probar es que a partir de las condiciones establecidas en el enunciado, se puede deducir que el valor del ángulo
α es 30º)Partimos de un triángulo rectángulo isósceles ABC. Puesto que el punto D ha de cumplir CD=CB, se ha de encontrar sobre el arco de circunferencia de centro C y radio CB. Elegimos un punto D sobre ese arco y trazamos los segmentos DC, DB y DA, formándose tres triángulos, uno de los cuales ya es isósceles (el BDC). Imponemos la condición de que < BCD= < DAC=
α.
Como
< ADC = 180 – < DCA – < DAC = 180 – (45–
α) – α = 180 – 45 = 135ºLo que queda por probar es que en el triángulo ADC el ángulo DAC es de 30º. Ésto se puede hacer, puesto que ese triángulo está completamente definido, pues conocemos el valor de un ángulo ( < CDA = 135º) y el valor o la relación entre dos lados, por ejemplo CD = 1 y CA = ![]() .
.
Utilizando el teorema de los senos:
![]() .
.
Por lo tanto: ![]() ;
;
De donde: ![]() .
.
Por lo tanto:
α = 30º.Q.e.d.
Comprobación:
(Conociendo que el valor de
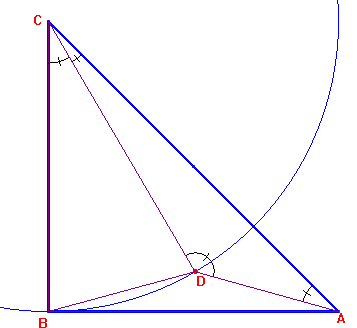
α va de ser de 30º y que, por tanto, el triángulo BDA es isósceles, situamos D sobre la mediatriz de BA. Entonces se comprueba que α vale 30º)Partimos de un triángulo rectángulo isósceles ABC. Puesto que el punto D ha de cumplir CD=CB, se ha de encontrar sobre el arco de circunferencia de centro C y radio CB.
Trazamos la mediatriz de AB y donde corte al arco de circunferencia trazado antes, situamos el punto D. Probaremos ahora que es
α =30º.< DBC = (180–
α α)/2 = 90 – α/2Por lo tanto: < DBA =
α/2Como el triángulo BDA es isósceles: < DAB =
α/2Según las hipótesis del enunciado, < DAC =
αSe tiene entonces que, mirando el vértice A:
α/2 + α = 45º.Por lo que
α = 30º.