Solución al problema N° 49

Desde los vértices A y B de un cuadrado ABCD se trazan en el interior del cuadrado unas lineas rectas que forman ángulos de 15º con AB. Estas dos rectas se cortan en M. Demostrar que el triángulo DCM es equilátero.

De acuerdo el enunciado del problema construimos la figura siguiente

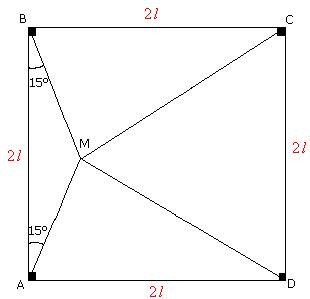
Ahora bien usando esta figura por el punto M tracemos una paralela a los lados BC y AD del cuadrado (de lado )

Esta paralela corta a AB en Q y a CD en Q entonces PQ = .

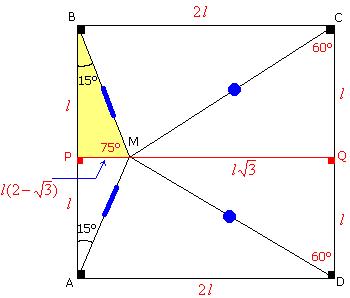
Para ver mejor esto veamos la siguiente figura:

En la figura notamos que el ser D BMA isósceles (BM = MA) entonces P es punto medio de AB luego: BP = PA =.

Por congruencia D BMC es congruente D DCM (criterio LLL) luego el D DMC es isósceles (MC = MD) y por tanto

Q es punto medio de CD entonces : CQ= QD = .

D BPM es notable (15°-75°) entonces de la figura: ....(1) y .....(2)

Despejando “k” de (1) y sustituyendo en (2):

Por tanto

Finalmente se deduce que D MQC es notable (30°-60°):

En consecuencia D DMC es EQUILÁTERO

Julio A. Miranda Ubaldo (Perú)