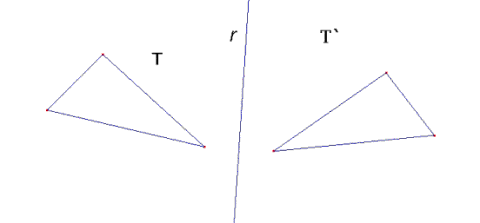
Problema 50
| Demostrar que dando sólo dos «cortes rectos» a cualquier triángulo T, y dada cualquier recta r, se puede descomponer en tres figuras geométricas (dos triángulos y un cuadrilátero) que pueden ser «reagrupadas» usando sólo rotaciones y traslaciones (no simetrías) construyendo T (triángulos simétrico de T respecto a r). |
Solución de la profesora Mª Luisa Fiol (Universidad Autónoma de Barcelona)
1 - Se trazan en cada uno de los triángulos dos alturas correspondientes.

Por ejemplo respecto a los lados de longitud mayor.
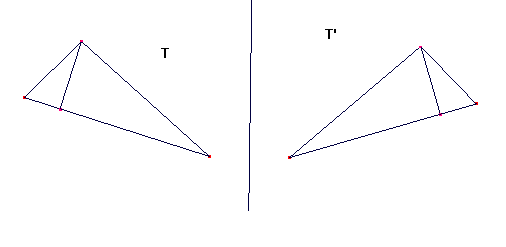
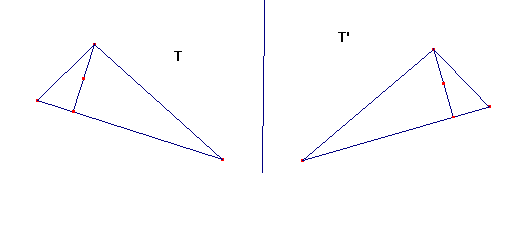
2 - Se localiza en cada caso el punto medio de las dos alturas.
3 - Se hace que el triángulo T ' gire 180º sobre este punto.
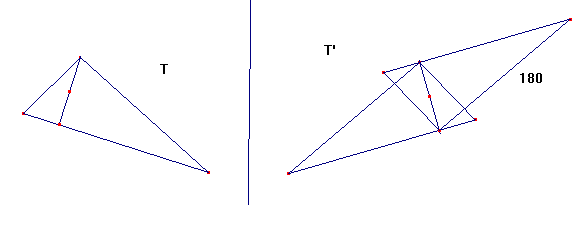
4 - Una vez hemos dado la vuelta al triángulo T ' se le desplaza (traslación y giro) hasta situarlo sobre T de forma que las alturas dibujadas coincidan y los lados que son bases correspondientes queden paralelos.
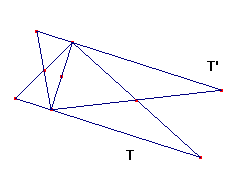
5 - Esto da sobre el triángulo T una descomposición en tres piezas: un cuadrilátero tipo cometa y dos triángulos isósceles.
Estos dos triángulos isósceles tienen cada uno un vértice que coincide con el punto medio de los dos lados del trángulo T.
Una vez obtenido el puzzle formado por las tres piezas, para pasar de T a T'
basta, si consideramos que las tres piezas forman el triángulo T, mantener fijo
el cuadrilátero y hacer girar 180º cada uno de los dos triángulos isósceles
con centro en sus vértices que coinciden con los puntos medios de los lados de T.
Al producirse estos giros se reproduce el triángulo T'.