Construir un triángulo dados el lado A, el lado B, y la altura HA . 1.Si se parte del lado A ; 2.Si se parte del lado B; 3.Si se parte de la altura HA

 

 

 

Santinelli R. y Siñeriz L.(1.999): CONSTRUCCIONES CON REGLA Y COMPÁS EN EL ENTORNO CABRI , comunicación presentada al Cabri World-99 de Sao Paulo CENTRO REGIONAL UNIVERSITARIO BARILOCHE UNIVERSIDAD NACIONAL DEL COMAHUE ARGENTINA

Solución de la alumnas Alicia y Maite Peña Alcaraz del Colegio Porta Celi de Sevilla al problema 52 (18 de Febrero de 2003)

1.      Si se parte del lado A:

Es fácil de explicar con un dibujo; que será lo que haremos:

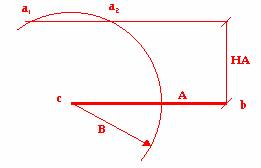Si nos dan el lado A, marcado con una línea más gruesa, basta hacer una paralela a A a distancia HA, y sobre esa recta estará a. Haciendo luego una circunferencia de radio B desde c, conseguimos los dos puntos donde podría estar a. Si hacemos la circunferencia en el otro lado, conseguimos los otros dos puntos a.

El triángulo pedido se consigue uniendo b con c y con a.

2.- Si se parte de B:

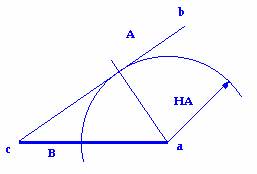Partiendo de B, desde el vértice al que se llame a, se hace una circunferencia de radio Ha, y desde el otro vértice se traza una tangente a dicha circunferencia. Esta tangente es el lado A, y donde acabe el lado A está el vértice b que faltaba.

(La tangente a una circunferencia desde un punto se hace con regla y compás uniendo el punto y el centro de la circunferencia, haciendo la mediatriz de ese segmento, y desde el punto medio, se hace una circunferencia que vaya hasta los dos extremos del segmento. Donde esa circunferencia corte a la anterior circunferencia está el punto de tangencia)

3. Si se parte de la altura HA:

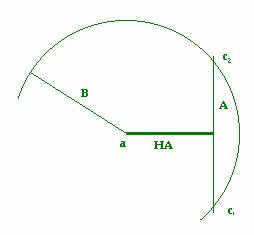Partiendo de HA, en el vértice a se hace una circunferencia de radio b y desde el otro extremo se hace una perpendicular que será A. El  punto de intersección de ambos será el vértice c (que como vemos hay dos). Prolongando luego el lado A hasta que mida lo que ha de medir se consigue el otro vértice b y se termina el triángulo.