Problema 58
Problema 58
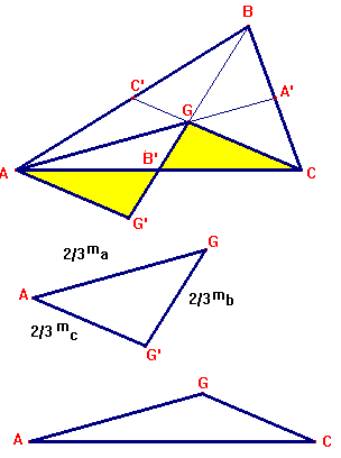
| El triángulo formado por las medianas tiene de área las tres cuartas partes del triángulo original. |
Nelsen, R.B. (2.000): Proofs without words II. MAA. Washington, DC. (pág 16).
Solución de F. Damián Aranda Ballesteros, profesor de matemátifcas del IES Blas Infante en Córdoba
| |
Dado el triángulo inicial ABC, y sus medianas ma , mb y mc, consideramos el triángulo formado por los segmentos 2/3×ma , 2/3×mb y 2/3×mc cuya superficie es igual a la del triángulo formado por el baricentro, G y dos vértices cualesquiera del triángulo original. Así este triángulo tendría como área 1/3 del área del triángulo ABC. (1) Por otro lado el área del triángulo de lados ma , mb y mc será igual a (3/2)2= 9/4 del área del triángulo de lados 2/3×ma , 2/3×mb y 2/3×mc. (2) Uniendo ambos resultados (1) y (2), obtenemos que el área del triángulo de lados ma , mb y mc será igual a 1/3×9/4 del área del triángulo ABC, es decir igual a 3/4 del área de este último. Area (ma, mb, mc) = 3/4 ×Area (a,b,c) |