PROBLEMA 58

Nicolás Rosillo.

Dpto. Matemáticas, IES Máximo Laguna.

Santa Cruz de Mudela, Ciudad Real

nrosillo@olmo.pntic.mec.es

El triángulo formado por las medianas tiene de área tres cuartas partes del triángulo original.

Sin pérdida de generalidad, se puede suponer una configuración como la siguiente:

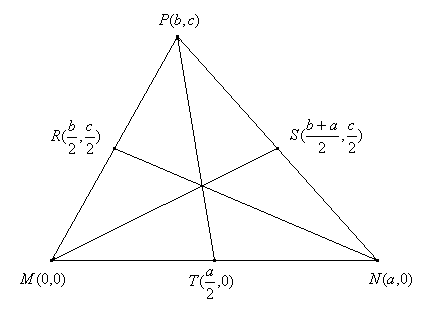
en la que se muestran tanto los vértices del triángulo como los puntos medios de los lados.

Dicho triángulo tiene por área

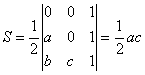
Se forman los vectores TP, SM y RN, de valores , y respectivamente.

Con ellos, se construye el triángulo formado por las medianas. Partiendo de un punto cualquiera (0,0) se traslada éste mediante el vector TP, obteniéndose el segundo vértice, de coordenadas , que a su vez se traslada mediante el vector SM, obteniéndose el tercer vértice del triángulo .

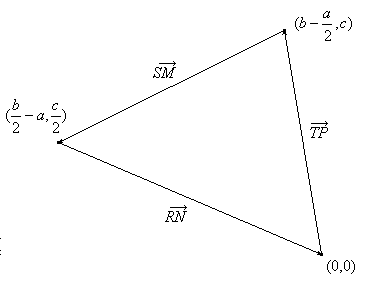
Si se calcula el área de este triángulo se obtiene el resultado deseado:

.
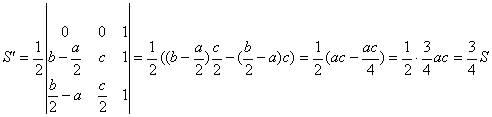