Problema 59

F. Damián Aranda Ballesteros

Sea c la longitud de la hipotenusa de un triángulo rectángulo, cuyos catetos miden a y b.

Demostrar que

¿Cuándo tiene lugar la identidad?

Sol 1.- (Algebraica)

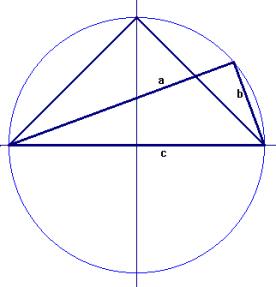
En el triángulo rectángulo de catetos a , b y de hipotenusa c, tenemos que:
c< a+b y además c² = a² + b².

De la desigualdad , (1) obtenemos esta otra equivalente: .

Si a ambos miembros de esta desigualdad le sumamos obtenemos:

;

De las anteriores consideraciones deducimos que, solamente se dará la igualdad en si en la desigualdad (1) se diera también la igualdad y esto únicamente sucederá cuando sean a y b iguales, o sea, el triángulo rectángulo sea isósceles.

Sol 2.- (Geométrica)

Como , se tiene que, para un valor fijo de la hipotenusa c, cuanto mayor sea el producto a×b, mayor también será la suma a+b. Ahora bien el producto a×b alcanzará su valor máximo cuando también sea máximo el valor alcanzado por 1/2×a×b o sea por el área del triángulo rectángulo de hipotenusa c fija y por catetos a y b. Pero esta área es máxima cuando lo sea la altura relativa al ángulo recto, h_c, valor que se alcanzará cuando h_c sea igual al radio de la circunferencia circunscrita al triángulo dado. Este valor del radio no es otro que . Solamente en este caso se da la igualdad siguiente a=b= y, por tanto a+b=. De modo que, en general, se tendrá la desigualdad