Sea c la longitud de la hipotenusa de un triángulo rectángulo, cuyos catetos miden a y b.
Demostrar que

¿Cuándo tiene lugar la identidad?

Nelsen, R.B. (2.000): Proofs without words II. MAA. Washington, DC. (página 12).

Solución del editor

Sea ABC el triángulo rectángulo con ángulo recto en C.

Construyamos el cuadrado ABDE de lado AB que contiene a C en su interior

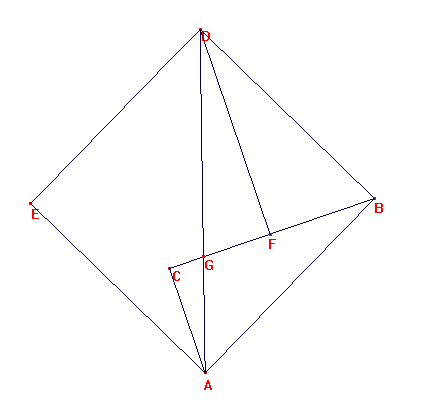
Construyamos el triángulo rectángulo en F BFD congruente al ACB

Sea AD la diagonal de ABDE que mide

AD corta a BC en G. Luego AD = AG + GD.

Consideremos los triángulos

AGC, que es rectángulo en C y en el que el cateto AC es menor que la hipotenusa AG. luego es b AG

De la misma maners, en el triángulo rectángulo BFG tensmos que a = BC = DF GD

Luego es: a+b AG + GD =, c.q.d.

¿Cuándo tendrá lugar la igualdad?

Tal y como se puede apreciar en esta resolución, los catetos AC y DF habrán de ser iguales a las hipotenusas AG y DG.

Ello tenbdrá lugar sólo cuando los triángulos rectángulos "degeneren" en los segmentos AG y DG, es decir, cuando

el punto C está sobre la diagonal del cuadrado construido, y por tanto el triángulo ABC sea isósceles, y

tenga de ángulos 45º, 45º, y 90º.

Ricardo Barroso