Homenaje al profesor Jordi Dou con motivo de su 90 cumpleaños

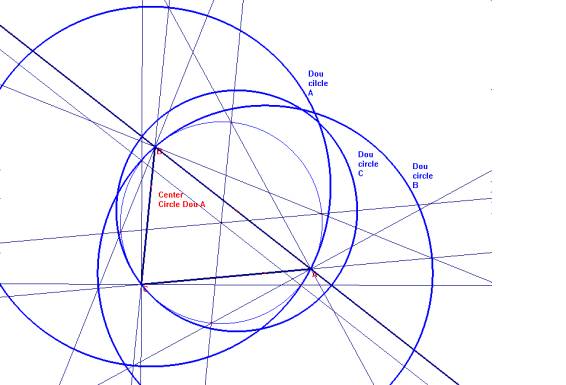
Dado el triángulo ABC, construir un círculo que corta(prolongado) a
las rectas BC, CA y AB en pares de puntos A' y A", B' y B" y C' y C"
respectivamente, tal que los ángulos A'AA", B'BB" y C'CC" son todos
ángulos rectos.

 
 
 Dou, J. 12(1986)79 Crux Mathematicorum 1140

Solución parcial del editor.

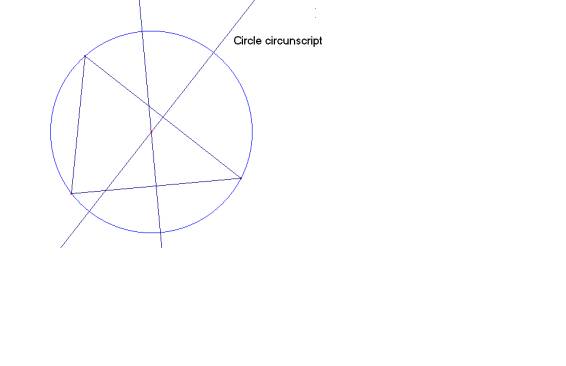
1.- Tracemos la circunferencia circunscrita

2.- Por el centro, tracemos una paralela a un lado BC

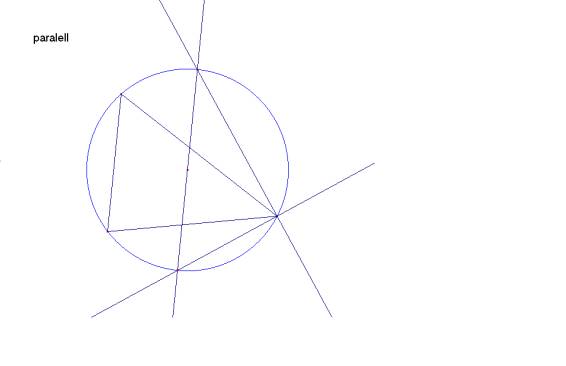
3.- Por el vértice A opuesto, tracemos las dos rectas que lo unen a los puntos de corte D E de la paralela

con la circunferencia.

4.- AD y AE Cortarán a la prolongación de BC en F y G.

5.- La circunferencia circunscrita a AFG cumple la condición. Hay tres, de distintos centros y radios

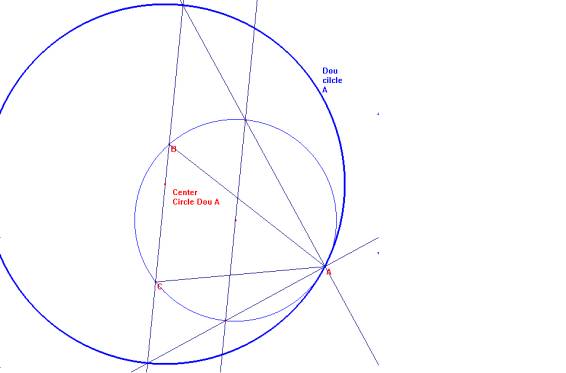
6.- Son: